En este artículo te voy a explicar qué es la recta presupuestaria, un concepto económico que te permitirá visualizar todas las posibilidades que se tienen de utilizar un determinado presupuesto. Además, te voy a mostrar un ejemplo sencillo y realista de cómo aplicar la recta presupuestaria para que el concepto te quede más claro.
¿Te interesa? Sigue leyendo y descubre cómo funciona la recta presupuestaria.
¿Qué es la recta presupuestaria?
Seguro que sabes lo difícil que puede ser controlar tus gastos cuando tienes una cantidad fija de dinero (ingresos) cada mes. Eso es lo que le pasa a nuestra consumidora hipotética, una mujer que tiene 100 dólares para gastar cada semana en alimentos y vestido. ¿Qué opciones tiene? ¿Qué combinaciones existen dado el presupuesto y el precio de los bienes?
Para responder a estas preguntas, vamos a usar un concepto muy útil: la recta presupuestaria. La recta presupuestaria muestra todas las posibilidades que se tienen de gastar una cantidad determinada de dinero (ingresos, renta, presupuesto, etc) en un conjunto de bienes o servicios diferentes a un precio determinado. En este caso, los bienes son los alimentos y el vestido.
¿Qué nos va ayudar a saber cuáles son las combinaciones de ropa y vestimenta con 100 dólares? La recta presupuestaria y como su nombre lo indica, se trata de nada más y nada menos que una recta.
Por lo cual, ya hemos encontrado otras de las utilidades de la ecuación de la línea recta, las cuales podemos utilizar en nuestra vida cotidiana. A continuación, voy a desarrollar el ejemplo paso a paso:
Ejemplo resuelto paso a paso
Las combinaciones de alimentos y vestido que la mujer puede comprar se van a encontrar en la siguiente recta:
Como ya sabes, hay diferentes formas para obtener la ecuación de la línea recta. En este caso, ya que tenemos dos puntos en el plano cartesiano, para obtener la ecuación de la línea recta voy a utilizar los dos puntos.
Por supuesto, ya que voy a utilizar esa forma, entonces voy a necesitar dos puntos como base. Bueno, vamos a seguir los siguientes pasos:
Paso 1: vestimenta es cero
Ya que queremos conocer todas las combinaciones posibles para gastar 100 dólares en comida y en vestimenta, es justo pensar que una de ellas consiste en gastar todo en comida y nada en vestimenta, ¿Cierto?
Si sustituimos la cantidad de vestimenta por 0 en la ecuación, eso nos deja con lo siguiente:
Esto queda de esta forma porque tienes que recordar que cualquier número multiplicado por 0 es 0. Por ende nos queda la ecuación así. Además, he sustituido la I con 100 porque es la cantidad fija de renta que recibe la mujer.
Ahora, vamos a suponer que el precio de los alimentos es de 1 dólar por unidad. Por lo cual, PA es igual a 1. Entonces, la única variable que nos queda es la cantidad de alimentos. Por lo tanto, es la que vamos a despejar y la vamos a despejar porque es la única cantidad que va a variar, claro que también va a variar la cantidad de vestimenta.
Es decir, la cantidad de alimentos es igual a 100.
Paso 2: alimentos es cero
Ahora, también es posible que la mujer decida gastar todo en vestimenta y nada en comida. Por lo cual, hacemos exactamente lo anterior, pensando que la vestimenta cuesta 2 dólares por unidad. Si hacemos lo mismo que antes, tenemos que llegar a que V (cantidad de vestimenta) es igual a 50.
Paso 3: definir punto A
Ahora sí podemos obtener los dos puntos que necesitamos. Para hacerlo, en primer lugar necesitamos definir nuestro plano cartesiano.
Como puedes ver, en el plano cartesiano he puesto en el eje de las Y a la cantidad de alimento y en el eje de las X a la cantidad de vestimenta.
Ahora bien, vamos a definir nuestro primer punto. Si no avanzamos en el eje X, y sólo avanzamos en el eje Y, eso quiere decir que no vamos a gastar en vestimenta y sólo vamos a gastar en alimento. ¿Cuánto? Todo nuestro presupuesto, el cual es de 100 dólares.
Ahora bien, tomando en cuenta el precio de los alimentos, ¿Cuánto podemos comprar de alimentos con los 100 dólares que tenemos? Esto ya lo hicimos en el paso uno y llegamos a la conclusión de que podemos obtener 100 unidades. Después de todo, cada unidad vale 1 dólar.
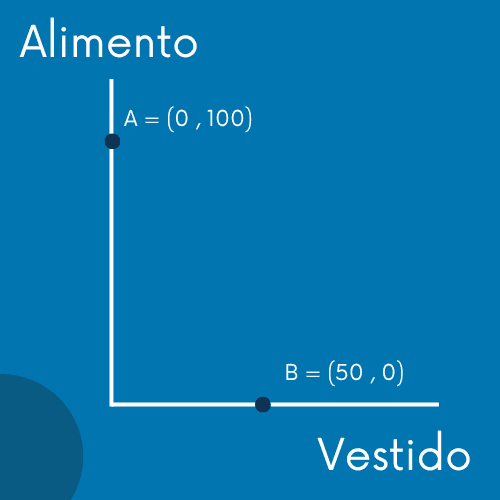
Así pues, nuestro primer punto, es decir el punto A queda como sigue: A = (0,100).
Paso 4: definir punto B
Ahora, vamos a suponer que no se compra alimento y sólo se compra vestimenta. Esto quiere decir que no avanzamos en el eje Y y sólo avanzamos en el eje X. ¿Cuánto? Eso lo hicimos en el paso 2. Si el precio de la vestimenta es de 2 dólares y tenemos 100 dólares, entonces sólo podemos comprar 50 unidades de vestimenta. ¿Cierto?
De tal forma que el punto B es es siguiente: B = (50 , 0)
Paso 6: obtener la ecuación de la recta que pasa por dos puntos
Se puede obtener la ecuación de la recta que pasa por dos puntos de manera manual, es decir utilizando la ecuación. Para fines prácticos y no hacer el artículo muy largo, ya que considero que eso sería para otro artículo, yo voy a utilizar Excel y voy a obtener la ecuación.
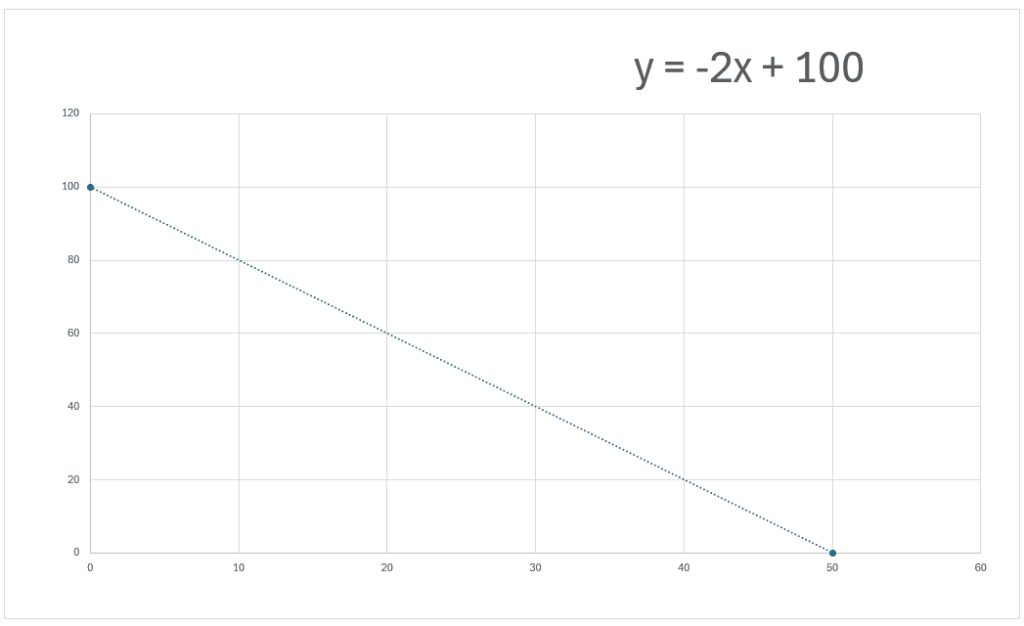
La recta y la ecuación de la recta son las siguientes:
De tal forma que la ecuación de la recta Y = -2x + 100 representa toda la combinación de puntos (bienes) que podemos adquirir con 100 dólares y con los precios establecidos en los productos. Como puse un ejemplo muy sencillo, podemos ver en la gráfica claramente de lo que hablo.
Nota: la ecuación puede interpretarse de la siguiente forma: A = -2V + 100. Recuerda que A es la cantidad de alimentos y V es la cantidad de vestimenta.
Vamos a tomar el punto C = (10 , 80). Este punto de la recta nos indica que con 100 dólares podemos adquirir 10 unidades de vestimenta y 80 unidades de alimento. ¿Será cierto? Vamos a sustituir los datos en la primera ecuación, es decir: I = PA A + PV V
Es decir:
- 100 = (1 * 80) + (2 * 10)
- 100 = 80 + 20
- 100 = 100
Ahora, vamos a suponer que quiero o necesito adquirir 20 unidades de vestimenta. ¿Cuánto necesito comprar de alimento? Vamos a utilizar la ecuación que nos otorgó excel, es decir, la ecuación de la recta.
Tenemos la siguiente ecuación. A = -2V + 100. Ya que quiero conocer la cantidad de alimento, ya no necesito despejar nada. Lo único que necesito es sustituir la cantidad de vestimenta en la ecuación y resolver.
- A = -2(20) + 100
- A = -40 + 100
- A = 60
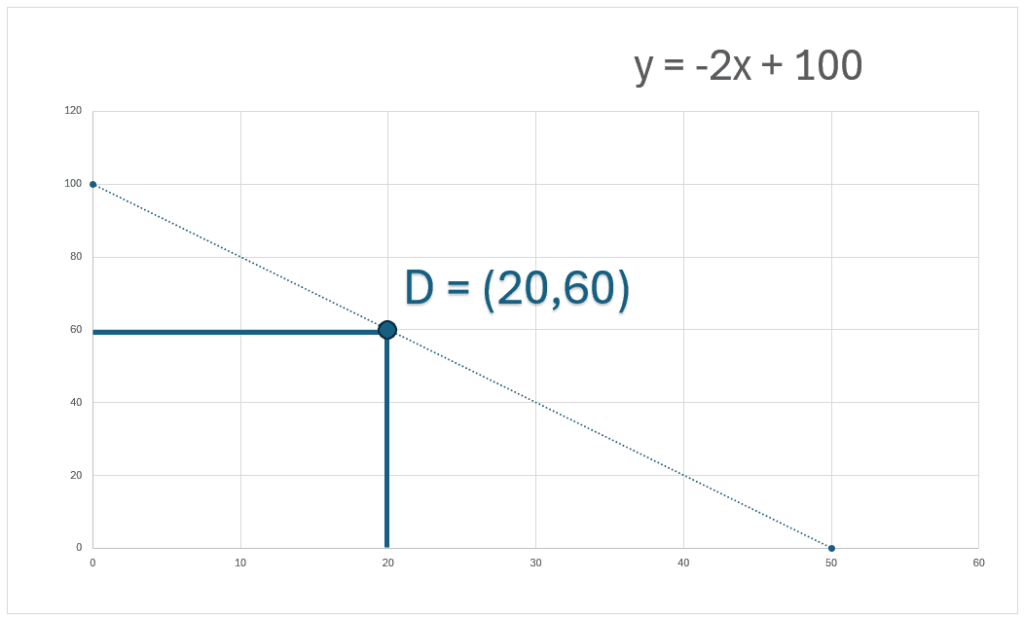
Por lo tanto, la cantidad de alimento es igual a 60. De tal forma que nuestro punto D = (20 , 60). Vamos a ver reflejado el punto D en la gráfica:
Si queremos hacer lo contrario y queremos conocer la cantidad de vestimenta, a partir de la cantidad de alimento, entonces despejamos V y resolvemos.
Ahora bien, como puedes ver, cada par ordenado de la recta nos otorga una posible combinación de alimento y vestimenta. Por ejemplo, otra posibilidad es la siguiente: E = (30, 40). De tal forma que se pueden adquirir 30 unidades de vestimenta y 40 unidades de alimento.
¿Qué pasa si varía la renta en la recta presupuestaria?
La variación en la renta produce un cambio en la ordenada al origen de la recta presupuestaria, pero la pendiente no cambia. Por lo tanto, las rectas resultantes de la variación van a ser paralelas a la recta original.
¿Qué pasaría si varían los precios en la recta presupuestaria?
Una variación en el precio de los bienes implicaría un cambio en la pendiente de la recta presupuestaria.
Conclusión
Una recta presupuestaria nos describe todas las posibles combinaciones de bienes que pueden adquirirse dada la renta del consumidor y los precios de los bienes.