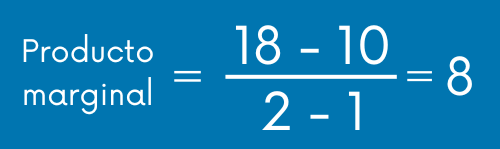¿Sabes qué es lo que hace que tu negocio crezca? No es solo la cantidad de recursos que inviertes, sino cómo los aprovechas. El producto marginal es una medida que te indica cuánto aumenta tu producción cuando añades una unidad más de trabajo, manteniendo el resto de factores constantes.
¿Qué es el producto marginal?
Como dije al principio del artículo, el producto marginal es una forma de medir cómo crece tu producción cuando añades más trabajo a tu negocio, sin cambiar nada más. Es decir, es el resultado de sumar una unidad más de trabajo (por ejemplo, un empleado más) y ver cuánto aumenta tu producción (por ejemplo, cuántos pasteles más puedes hacer).
Beneficios del producto marginal
Estos son algunos de los beneficios que el producto marginal te ofrece para tu empresa:
- Te ayuda a optimizar tu rendimiento y maximizar tus beneficios.
- Te permite saber si estás aprovechando al máximo tus recursos o si estás desperdiciando parte de ellos.
- Te facilita evaluar si te conviene contratar más personal, invertir en más maquinaria, cambiar tu forma de producir o buscar otras alternativas.
- Te da la posibilidad de tomar mejores decisiones para tu empresa, basadas en datos y no en intuiciones.
- Te hace mejorar tu eficiencia y tu productividad.
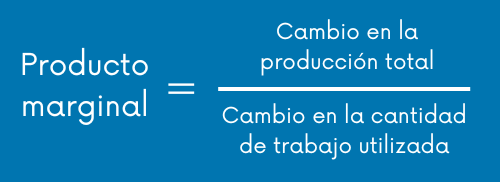
Fórmula para calcular el producto marginal del trabajo
¿Cómo sacar el producto marginal del trabajo? A continuación, te voy a proporcionar una fórmula para que puedas calcularlo de manera sencilla:
Para que quede más claro, a continuación te voy a poner un ejemplo y más adelante te voy a poner ejercicios resueltos. Así podrás ver que es muy sencillo resolver los problemas.
Ejemplo de producto marginal
Para entender mejor el producto marginal, vamos a usar el ejemplo de Ana, la dueña de una pastelería. Ana tiene un horno que le permite hacer 20 pasteles al día con un empleado. Si Ana quiere hacer más pasteles, tiene que contratar más empleados. Pero, ¿cuántos pasteles más puede hacer con cada empleado que contrata? Eso es lo que nos dice el producto marginal.
Mira la siguiente tabla
| Número de empleados | Producto total (pasteles) | Producto marginal (PM) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 20 | 20 |
| 2 | 42 | 22 |
| 3 | 52 | 10 |
| 4 | 57 | 5 |
| 5 | 57 | 0 |
El PM es el número que aparece en la última columna. Es el aumento del producto total (la segunda columna) cuando se añade una unidad más de trabajo (la primera columna). Por ejemplo, el producto marginal del primer empleado es de 20 pasteles: al contratar a un empleado, Ana puede hacer 20 pasteles al día. El PM del segundo empleado es de 22 pasteles: al contratar a otro empleado, Ana puede hacer 22 pasteles más al día, es decir, 42 pasteles en total.
¿Qué pasa cuando Ana contrata más empleados? El producto marginal va disminuyendo. Esto significa que cada empleado que contrata produce menos pasteles que el anterior. ¿Por qué? Bueno, se debe a diferentes factores, sin embargo, recuerda que sólo estamos incrementando el trabajo (en este caso trabajadores) y todo lo demás sigue igual. Por lo tanto, tenemos un horno para muchos trabajadores.
Así pues, aunque aumentemos de trabajadores, llega un punto en que la producción adicional por trabajador deja de aumentar y comienza a disminuir.
¿Qué lección podemos sacar de este ejemplo?
Que el producto marginal nos muestra cómo optimizar nuestra producción y maximizar nuestros beneficios.
Si contrata más empleados de los que necesita, está desperdiciando su recurso de trabajo y pagando salarios innecesarios. Ana también podría invertir en otro horno o en un horno más grande, para aumentar su capacidad de producción y su producto marginal.
Por cierto, en este ejemplo, posiblemente la cantidad adecuada de trabajadores podría ser de 2.
¿Te ha quedado claro lo que es el producto marginal? Espero que sí. Es un concepto muy útil para mejorar tu negocio y hacerlo crecer.
Ejercicios resueltos de producto marginal
A continuación, te voy a poner un par de ejercicios resueltos para que puedas aplicar lo que has aprendido. Espero que te sean de utilidad.
Ejercicio 1
Una empresa produce zapatos usando dos factores de producción: trabajo y capital. La siguiente tabla muestra la relación entre el número de trabajadores, el número de máquinas y la producción total de zapatos por día.
| Número de trabajadores | Número de máquinas | Producto total (zapatos) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 10 |
| 2 | 1 | 18 |
| 3 | 1 | 24 |
| 4 | 1 | 28 |
| 5 | 1 | 30 |
Se pide calcular el producto marginal del trabajo, manteniendo constante el otro factor.
Solución del ejercicio
Para calcular el producto marginal del trabajo, tenemos que ver cómo cambia la producción total al variar el número de trabajadores, manteniendo constante el número de máquinas. Usando la fórmula, tenemos que:
Vamos a utilizar la fórmula para sacar el PM para 2 trabajadores:
Como puedes ver, lo que se hace es producto total final menos el producto total inicial (18 – 10) y lo dividimos entre el número de trabajadores final menos número de trabajadores inicial (2-1).
Ya que sacamos para dos trabajadores, si sacamos el resto obtenemos lo siguiente:
| Número de trabajadores | Producto total (zapatos) | Producto marginal |
|---|---|---|
| 0 | 0 | – |
| 1 | 10 | 10 |
| 2 | 18 | 8 |
| 3 | 24 | 6 |
| 4 | 28 | 4 |
| 5 | 30 | 2 |
Con los resultados obtenidos ya podemos tomar mejores decisiones sobre cuántos trabajadores son necesarios contratar.
Ejercicio 2
Una granja produce leche usando dos factores de producción: vacas y pasto. La siguiente tabla muestra la relación entre el número de vacas, la cantidad de pasto y la producción total de leche por día.
| Número de vacas | Cantidad de pasto (kg) | Producto total (litros) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 10 | 20 |
| 2 | 20 | 35 |
| 3 | 30 | 45 |
| 4 | 40 | 50 |
| 5 | 50 | 52 |
Se pide calcular el PM de las vacas, manteniendo constante el otro factor.
Solución del ejercicio
Para calcular el producto marginal de las vacas, tenemos que ver cómo cambia la producción total al variar el número de vacas, manteniendo constante la cantidad de pasto. Usando la fórmula, tenemos que:
| Número de vacas | Producto total (litros) | Producto marginal de las vacas (litros) |
|---|---|---|
| 0 | 0 | – |
| 1 | 20 | 20 |
| 2 | 35 | 15 |
| 3 | 45 | 10 |
| 4 | 50 | 5 |
| 5 | 52 | 2 |