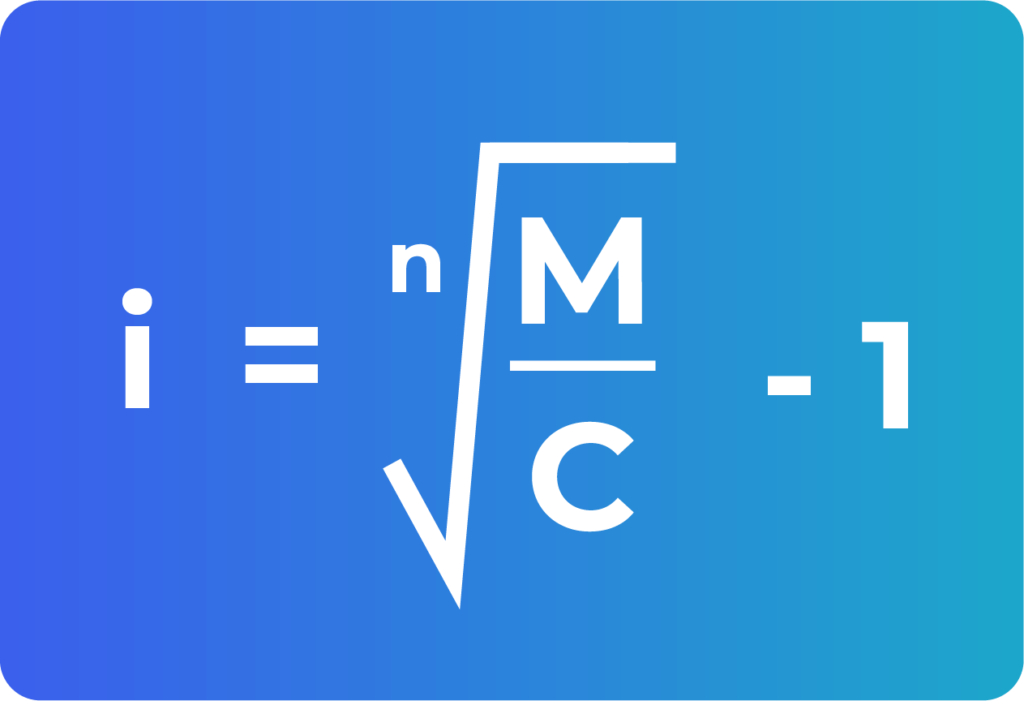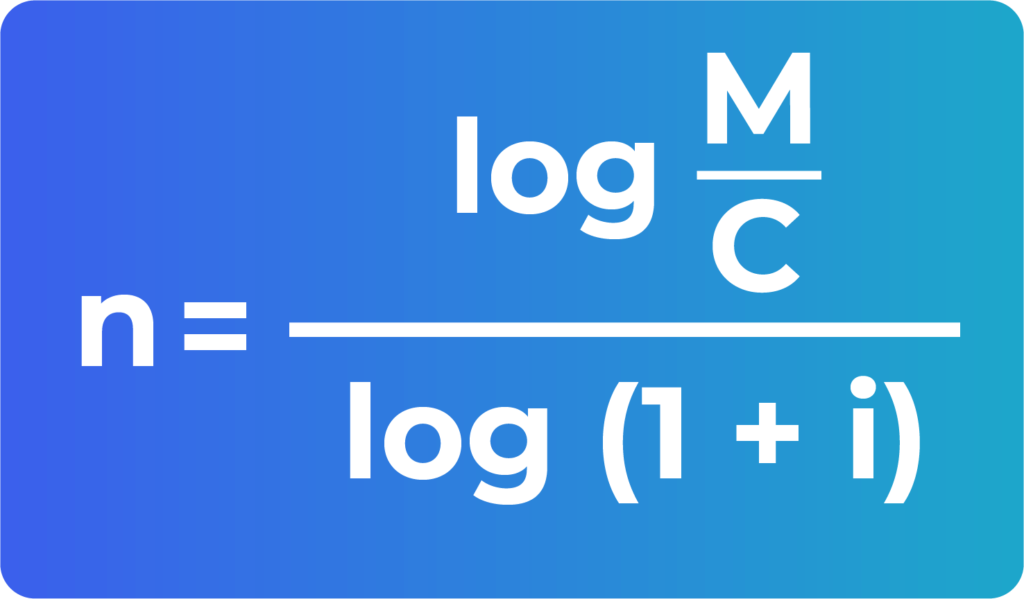Ya que sabes lo que es el interés compuesto y que ya sabes lo que es una tasa nominal, efectiva y equivalente; entonces es tiempo de resolver algunos ejercicios de interés compuesto. Espero que te sean de utilidad.
Al final del artículo encontrarás una calculadora de interés compuesto, la cual te servirá para poder calcular la tasa de interés, el tiempo, el monto, el capital y el interés. De tal forma que sólo hace falta que ingreses los datos y que pulses un botón para que puedas calcular interés compuesto.
Comentario inicial
Recuerda que para que puedas resolver los siguientes ejercicios, tienes que conocer el funcionamiento del interés compuesto y tienes que conocer lo que son las tasas nominal, efectiva y equivalente.
Una vez que ya lo sabes, puedes continuar con el artículo. Asimismo, yo te recomiendo que intentes resolver los ejercicios tú mismo y que luego compares las respuestas.
¡Aprende qué es el interés compuesto!
¡Leer más!¡Aprende sobre tasa nominal, efectiva y equivalente!
¡Leer más!Fórmulas para resolver los ejercicios de interés compuesto
En el artículo que te sugerí anteriormente podrás encontrar las diferentes fórmulas de interés compuesto, sin embargo, considero que puede serte de utilidad tener una especie de formulario.
Por lo cual, para que se te haga un poco más fácil resolver los ejercicios de interés compuesto, entonces te voy a dejar una imagen con todas las ecuaciones que vas a necesitar.
Recuerda que no necesitas memorizar todas, ya que basta con memorizar una y las demás puedes obtenerlas cuando quieras. Lo único que necesitas hacer es despejar. Bueno, tengo que aclarar que la primera ecuación sí es diferente.
Aunque, es de cierta forma de sentido común, ya que si al monto o valor futuro le restamos el capital o valor presente, entonces obtenemos los intereses generados.
Regla importante a tomar en cuenta para poder resolver bien los ejercicios
Es muy importante tener en cuenta que el tiempo y la tasa de interés deben de estar expresadas en la misma unidad de medida. De tal forma que si la tasa de interés que tienes es mensual, entonces el tiempo también lo tienes que manejar mensualmente.
Por lo cual, si en algún problema tienes el tiempo y la tasa de interés en unidades diferentes, entonces tienes que convertir una unidad para que ambas estén en la misma unidad.
Ejercicios de Interés compuesto
Ahora sí vamos a empezar con los ejercicios resueltos de interés compuesto. A continuación, te voy a dejar 14 ejercicios resueltos de interés compuesto para que puedas practicar. Además, te voy a dejar una calculadora de interés compuesto para que puedas resolver tus ejercicios.
Espero que te sean de utilidad y recuerda que puedes dejarme tus dudas en los comentarios.
Ejercicio 1 de interés compuesto: Obtener el capital
Emmanuel quiere comprar una casa que cuesta $1,000,000. Si le pidieron que entregue 50% de anticipo y 50% en un plazo de dos años, al término de la construcción y entrega del inmueble. ¿Cuánto dinero tiene que depositar en el banco en este momento para poder garantizar la liquidación de su adeudo en el plazo correspondiente? Considera que la tasa de interés es del 10% anual capitalizable mensualmente.
Solución del ejercicio 1
Bueno, el problema nos está diciendo que Emmanuel quiere invertir hoy una cantidad x en el banco, la cual deberá de generarle intereses y con los cuales podrá liquidar su adeudo en 2 años. Es decir, va a invertir hoy una cantidad de dinero y lo dejará ahí por dos años. Cuando tenga que pagar el dinero, (en 2 años) únicamente tendrá que retirar su dinero y pagar la deuda.
Ahora bien, sabemos que en 2 años tenemos que pagar $500,000. Esto es debido a que es el 50% de la cantidad acordada. Si queremos conocer lo que tenemos que invertir hoy para que en dos años podamos recibir $500,000. Entonces, vamos a utilizar la ecuación de capital.
La ecuación de capital es la siguiente:
Ahora, vamos a sustituir los datos que tenemos en la ecuación de capital:
Por lo cual, el resultado es: $409,704.77
- En este problema nos vamos a enfrentar con el hecho de que la tasa de interés y el tiempo tienen que estar en la misma unidad de medida. En este problema nos dan el tiempo en años y la tasa de interés no es anual, sino que capitaliza mensualmente. Por lo cual, tenemos que convertir uno de los dos para que estén en la misma unidad. Para que sea más fácil, yo convertí los 2 años a meses (24 meses).
- Cabe destacar que, en interés compuesto se tiene que convertir la tasa de interés que nos dan en una tasa equivalente. La tasa equivalente es de 0.1047 o 10.47% anual. Si deseas aprender sobre tasa nominal, efectiva y equivalente, entonces pulsa el siguiente enlace:
En conclusión, si hoy voy al banco e invierto $409,704.77 pesos a una tasa de interés del 10% anual capitalizable mensualmente por 2 años, entonces voy a ser capaz de obtener $500,000 pesos.
Cabe destacar que las dos ecuaciones son iguales y la puse porque puedes encontrar ambas formas en los libros. Puedes sustituir los datos en la primera ecuación y verás que el resultado es el mismo.
Nota: Si quieres comprobar que realmente es la cantidad que deseas, puedes utilizar la ecuación de monto. Utilizando como capital los $409,704.77. Asimismo, tienes que tomar en cuenta que no estoy utilizando todos los decimales. Si quieres que tu resultado sea exacto, entonces tienes que tomar todos los decimales.
Ejercicio 2 de interés compuesto
¿Cuánto producirá de interés un capital de $10,000 impuesto al 9% semestral en 5 años?
Solución del ejercicio 2
En primer lugar, tienes que recordar que el interés es igual al monto menos el capital. Ahora bien, ya tenemos el capital, (10,000), tenemos que sacar el monto. La ecuación de monto es la siguiente:
Tengo que decir que es un ejercicio sencillo, pero tiene una pequeña trampa. Esto lo digo debido a que la tasa es semestral y el tiempo está en años. Aquí puedes usar lo que aprendiste de tasas y encontrar la tasa equivalente a un año. Si haces eso puedes utilizar el tiempo (n) como 5.
También puedes dejar la tasa como está y utilizar la n en semestres. Tú decides la forma en que deseas resolverlo. Por supuesto, puedes hacerlo de ambas formas para que puedas comprobar que te da el mismo resultado.
El resultado es: 23,673.636
Por último, lo que tenemos que hacer es restar el capital al monto, es decir, 23,673.636-10,000 = $13,673.636. Ese es el interés que se va a producir en 5 años.
Ejercicio 3 de interés compuesto
¿Qué interés producirá un capital de $25,000 al 36% anual en 4 años?
Solución del ejercicio 3
En este caso, sí podemos utilizar la ecuación de monto sin tener que utilizar una tasa equivalente o modificar el tiempo.
El resultado es: 85,525.50
El interés es igual a 85,525.5 – 25,000 = 60,525.50
Ejercicio 4 de interés compuesto
¿Qué interés producirá un capital de $25,000 al 16.619% semestral en 4 años?
Solución del ejercicio 4
Yo sé que es muy similar al anterior, pero esa es la intención. Esto es debido a que quiero que veas que las dos tasas que se manejan son equivalentes.
El resultado es: 85,525.28. Por cierto, yo sé que sale .28 y no .50. Esto es porque no se usaron todos los decimales. Cuando se saca la tasa equivalente con todos los decimales, sale: 0.166190379. Si utilizas esa tasa, sí vas a obtener el mismo resultado.
Por último, se tiene que hacer la resta: 85,525.28 – 25,000 = 60,525.28. Por supuesto, si utilizas todos los decimales de la tasa, entonces, la resta será de 85,525.50 – 25,000 = 60,525.50
Nota: como puedes ver, las tasas equivalentes te dan un monto igual. Además, es importante que veas que si no utilizas todos los decimales, tu resultado no va a ser muy exacto.
Ejercicio 5 de interés compuesto
Encuentre la tasa de un monto de $67,614.74, producido por un capital de $16,842.32 en 4 años.
Solución del ejercicio 5
Ya que nos están pidiendo encontrar la tasa, entonces, vamos a utilizar la ecuación de tasa. La ecuación de tasa es la siguiente:
Si sustituimos los datos, tenemos lo siguiente:
El resultado es de: 41.5499%
Ejercicio 6 de interés compuesto
Se desea saber el tiempo de una inversión, si como capital se impusieron $70,000 al 30% anual y originó un monto de $259,905.10.
Solución del ejercicio 6
En este caso nos están pidiendo el tiempo, por lo cual, tenemos que utilizar la ecuación del tiempo en interés compuesto:
Sustituyendo los datos en la ecuación del tiempo nos queda lo siguiente:
La respuesta es: 5 años.
Ejercicio 7
Supongamos que tenemos una inversión inicial de $10,000 con una tasa de interés anual del 5%. ¿Cuál será el valor de la inversión después de 3 años, si el interés se capitaliza mensualmente?
Solución del ejercicio 7
Primero, debemos recordar que la tasa que nos están dando es una tasa anual que capitaliza mensualmente. Por lo cual, no podemos poner 0.05 en la ecuación. Lo que hay que hacer es dividir 0.05 entre 12 (porque un año tiene 12 meses).
Ahora bien, ya que este ejercicio nos está pidiendo calcular el monto, entonces vamos a usar la ecuación para encontrar el monto en interés compuesto, la cual es:
M = C(1+i)^(n)
Al sustituir los valores en la ecuación obtenemos lo siguiente:
M = 10,000*(1+0.05/12)^(36)
M = $11,614.72
Por lo tanto, el valor de la inversión después de 3 años sería de $11,614.72
Ejercicio 8
Supongamos que queremos tener $15,000 dentro de 5 años y nos dicen que podemos obtener una tasa de interés anual del 7%, capitalizada mensualmente. ¿Cuál es la cantidad de dinero que debemos invertir hoy?
Solución del ejercicio 8
En este ejercicio nos están pidiendo que encontremos el capital. Por lo cual, lo que tenemos que hacer es utilizar la fórmula de capital en interés compuesto. La ecuación es la siguiente:
C = M/(1+i)^(n)
Si sustituimos los datos obtenemos lo siguiente:
- C = 15000/(1+0.07/12)^(60)
- C = 10581.07
Por lo tanto, debemos invertir $10581.07 hoy para obtener $15,000 dentro de 5 años.
Ejercicio 9
Supongamos que invertimos $5,000 a una tasa de interés anual del 8%. Si queremos que nuestra inversión crezca a $10,000, ¿cuántos años debemos esperar?
Solución del ejercicio 9
Ya que claramente nos están pidiendo que encontremos el tiempo, vamos a utilizar la fórmula para calcular el tiempo en interés compuesto, la cual es la siguiente:
n = log (M/C) / Log (1 + i)
Si sustituimos los datos obtenemos lo siguiente:
- n = log (1000/5000) / Log (1 + 0.08)
- = 9.0064 años.
Por lo tanto, debemos esperar aproximadamente 9 años para que nuestra inversión crezca a $10,000.
Ejercicio 10
Supongamos que invertimos $10,000 durante 5 años y obtenemos $15,000 al final del plazo. ¿Cuál fue la tasa de interés anual que obtuvimos?
Solución del ejercicio 10
Ya que nos están pidiendo que encontremos la tasa de interés, entonces vamos a usar la ecuación para calcular la tasa de interés en interés compuesto.
¿Cuál es la respuesta al ejercicio anterior?
La respuesta es: 0.0844717712 o el 8.4471%
Ejercicio 11: Calcular el monto
Andrea ha decidido invertir $5000 en una cuenta de ahorros que ofrece una tasa de interés compuesto del 8% anual. ¿Cuál será el monto total después de 3 años?
Sustituyendo los datos en la ecuación de monto obtenemos lo siguiente:
Por lo tanto, si calculamos el monto, obtenemos como resultado que Andrea va a recibir 6298.56 pesos en 3 años.
Ejercicio 12: Calcular el capital
Juan desea tener $10000 en su cuenta de ahorros dentro de 5 años, si la tasa de interés es del 12% semestral. ¿Cuánto dinero debe invertir hoy?
En el caso del ejercicio 12, lo que nos están pidiendo calcular es el valor actual o también llamado capital. Por lo cual, para poder resolver el problema, vamos a tener que sustituir los datos que nos dieron en la ecuación de capital.
Por lo tanto, Juan tiene que invertir el día de hoy 3219.73 pesos para poder obtener 10000 pesos en 5 años.
Ejercicio 13: Calcular el tiempo
María invierte $2000 en una cuenta de ahorros que ofrece una tasa de interés compuesto del 4% anual. ¿Cuánto tiempo tardará su inversión en crecer a $2500?
Para resolver este ejercicio, vamos a necesitar la fórmula del tiempo en interés compuesto. Si sustituimos los datos en la ecuación, obtenemos lo siguiente:
Por lo tanto, se tardarán 5.68 años en hacer crecer su inversión. Algo a destacar es que el tiempo lo vamos a a obtener en la misma unidad de medida en que está nuestra tasa. De tal forma que si nuestra tasa es anual, entonces el tiempo estará en años. Si nuestra tasa es mensual, entonces el tiempo será mensual.
Ejercicio 14: Calcular la tasa de interés
Carlos invierte $3000 en una cuenta de ahorros y después de 3 años, el monto total es de $7500. ¿Cuál es la tasa de interés anual?
En este caso, es necesario utilizar la ecuación para calcular la tasa de interés. Si sustituimos los datos en la ecuación, obtenemos lo siguiente:
Calculadora de interés compuesto para resolver ejercicios
A continuación, podrás encontrar una calculadora muy simple que te permitirá resolver cualquier ejercicio o problema de interés compuesto que se te presente.
¿Cómo funciona la calculadora? Bueno, podríamos decir que no es una sola calculadora, sino que son 5, las cuales te ayudarán a calcular el monto, el capital, el tiempo, la tasa de interés e inclusive el interés.
Lo único que tienes que hacer es identificar lo que te están pidiendo calcular e ingresar los datos necesarios en el apartado indicado. Una vez que has ingresado los datos, sólo tienes que pulsar en el botón de calcular y obtendrás tu resultado.
Algo muy importante a destacar es el hecho de que tienes que recordar que el tiempo y la tasa de interés deben de estar expresadas en la misma unidad de medida. Es decir, si la tasa de interés es mensual, entonces el tiempo también tiene que ser mensual. Si tienes problemas en los que no es así, entonces conviertes uno de los datos para que estén en la misma unidad de medida.
Calculadora de Monto
Calculadora de Tasa de Interés
Calculadora de Capital
Calculadora de Tiempo
Calculadora de Interés
Artículos que te pueden interesar

¿Qué es el interés simple?
¿Cansado de la complicada jerga financiera? Te invito a que descubras cómo funciona el interés simple mediante diferentes ejercicios resueltos. Pulsa el siguiente botón y comienza aprender.
¿Qué son las anualidades vencidas?
Ya que sabes sobre interés compuesto, entonces es tiempo de dar un paso adelante en el mundo de las matemáticas financieras y es tiempo de que empieces a aprender sobre las anualidades vencidas.