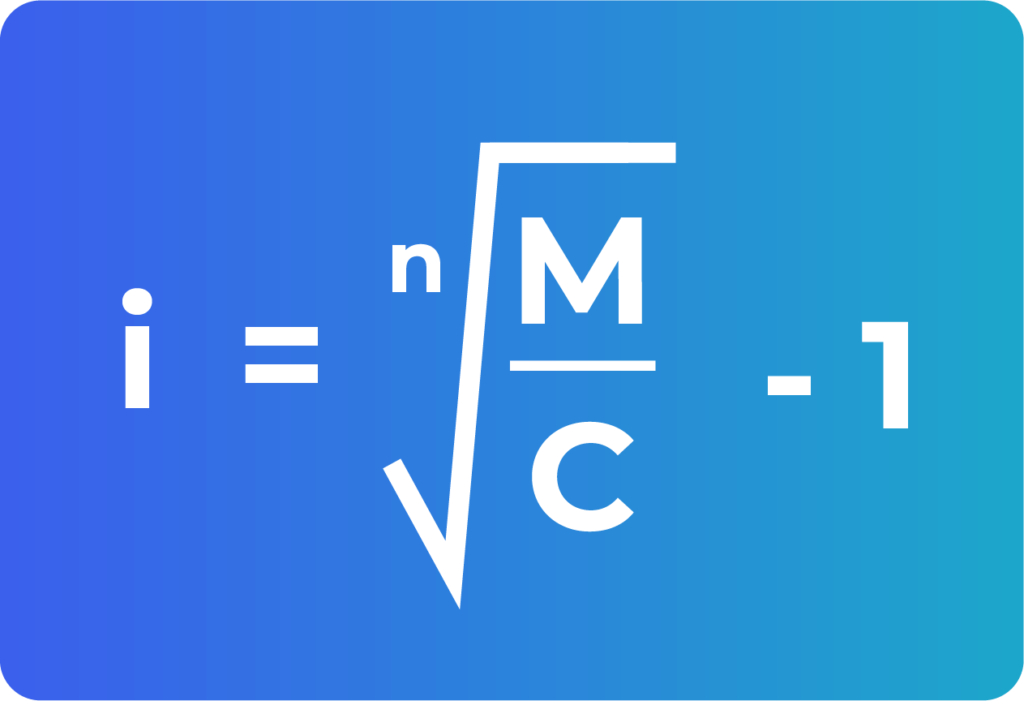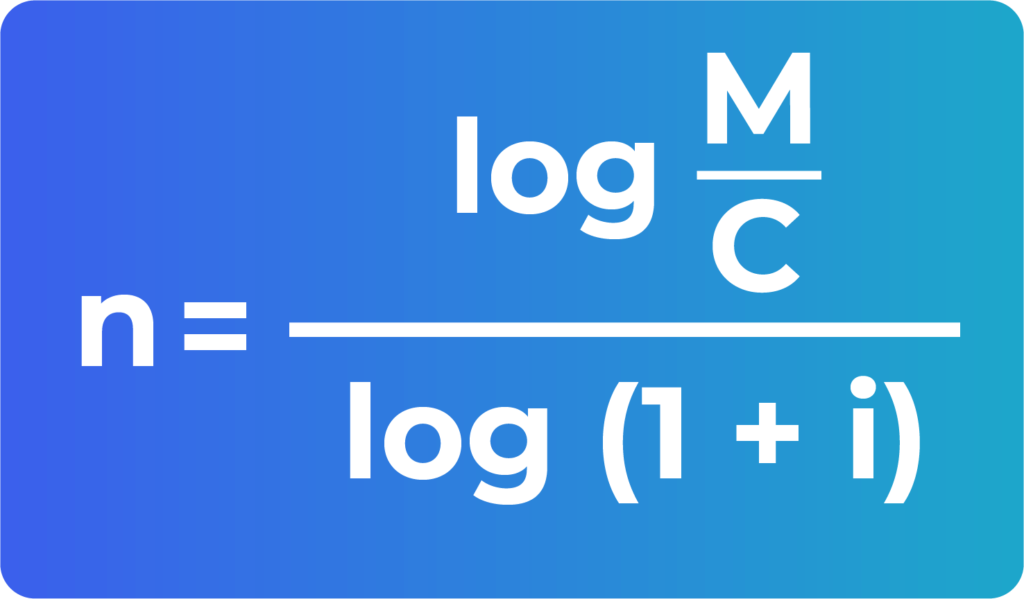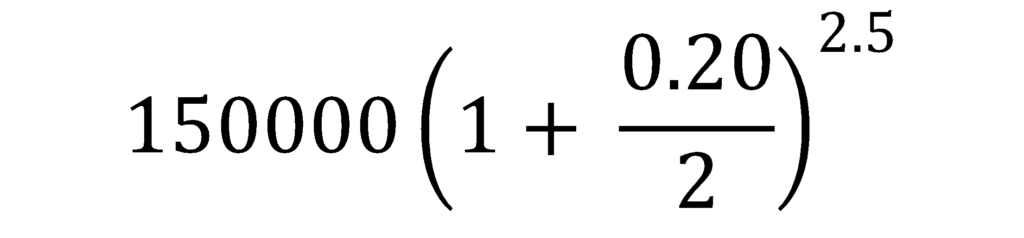Una vez que conoces lo que es el interés simple y cómo funciona, es tiempo de que subas de nivel y aprendas sobre el funcionamiento del interés compuesto.
Definición de interés compuesto según autores
A continuación, con el objetivo de que empieces a percibir lo que es el interés compuesto, te voy a poner algunas definiciones. Por supuesto, al final podrás ver la bibliografía. Asimismo, antes de pasar a ver lo que es el interés compuesto, tienes que conocer lo que es el interés simple.
Si deseas conocer lo que es el interés simple, puedes ir al siguiente artículo: ▷ Interés simple ◁
Definición según Díaz Mata Alfredo y Aguilera 👈
«Es la operación financiera en la que se capitalizan (se incrementa al capital original invertido) los intereses ganados, en periodos previamente acordados, con lo cual, a su vez, generan nuevos intereses»
(Díaz, Mata, Alfredo y Aguilera, 2020, p. 71)
Definición según Héctor Manuel Vidaurri Aguirre 👈
«El interés compuesto se puede definir como la operación financiera en la cual el capital aumenta al final de cada período por adición de los intereses vencidos»
(Vidaurri, Aguirre, Héctor, Manuel, 2017, p. 182)
Definición según Álvarez Arango Alberto 👈
«A diferencia del interés simple, aquí se suman periódicamente los intereses más el capital. Este proceso de sumar los intereses al capital cada vez que se liquidan se llama capitalización, y el periodo utilizado para liquidar los intereses se llama periodo de capitalización»
(Álvarez, Arango, Alberto, 2005, p. 8)
¿Qué es el interés compuesto?
En el interés simple, el capital siempre es el mismo, es decir, se mantiene constante. Por otra parte, en el interés compuesto, el capital va cambiando su valor con el tiempo. El capital va cambiando debido a que los intereses se van sumando al capital.
Explicación con ejemplo
Para que puedas ir viendo el funcionamiento del interés compuesto, voy a empezar con un ejemplo: supongamos que tenemos $100 pesos y lo queremos invertir a una tasa del 30% mensual (compuesta).
En la tabla usé la fórmula de monto de interés simple. Lo estoy haciendo así para que puedas relacionar el interés simple con el interés compuesto. Por supuesto, con sus modificaciones correspondientes, por ejemplo, en el tiempo.
Como puedes ver, los intereses se suman al capital y se va generando un nuevo monto cada mes que pasa y se mantendrá así el tiempo que se requiera. Cabe destacar que digo cada mes debido a que es así en este ejemplo, pero, no siempre será cada mes.
Ahora voy a poner una tabla en la que se muestra la forma en que se va comportando el interés compuesto.
| M1 = C(1 + i) |
| M2 = C(1 + i)(1 + i) |
| M3 = C(1 + i)(1 + i)(1 + i) |
| M4 = C(1 + i)(1 + i)(1+ i)(1 + i) |
A continuación, voy a sustituir los datos del ejemplo anterior para que puedas ver que es verdad.
| M1 = 100(1 + 0.30) = 130 |
| M2 = 100(1 + 0.30)(1 + 0.30) = 169 |
| M3 = 100(1 + 0.30)(1 + 0.30)(1 + 0.30) = 219.7 |
| M4 = 100(1 + 0.30)(1 + 0.30)(1 + 0.30)(1 + 0.30) = 285.6 |
Lo que quiero que veas de la tabla anterior es que el monto del primer mes se convierte en el capital del segundo mes y el monto del segundo mes se convierte en el capital del tercer mes. Por supuesto, así seguirá hasta que se necesite. En pocas palabras, queda de la siguiente forma:
| M1 = C(1 + i) |
| M2 = M1(1 + i) |
| M3 = M2(1 + i) |
| M4 = M3(1 + i) |
Siguiendo esa lógica es como podemos simplificar las multiplicaciones quedando con un exponente. La fórmula que obtenemos es la siguiente:
Respuesta del ejemplo con la fórmula de monto en interés compuesto
Si utilizamos la fórmula de monto que hemos obtenido, la cual es la fórmula que se utiliza en interés compuesto, obtenemos lo siguiente:
Como puedes ver, llegamos al mismo resultado que hemos estado obteniendo. Cabe destacar que la n es el tiempo. En este caso es 4 debido a que son 4 meses lo que se dejó el dinero. Por lo cual, al cabo de 4 meses recibirías $285.6 pesos si inviertes $100 a una tasa del 30%.
Conceptos necesarios
Como ya has podido notar, es necesarios que cuentes con algunas bases para que puedas entender lo que es el interés compuesto. Hay conceptos que ya debes de conocer, debido a que ya deberías de conocer lo que es el interés simple.
Ahora bien, voy a hablar de algunos conceptos que son nuevos y que se van a necesitar para que podamos comenzar a resolver problemas.
Periodo de capitalización:
Es el periodo convenido para convertir el interés en capital. Por ejemplo, si una operación se capitaliza trimestralmente, quiere decir que cada tres meses los intereses generados se agregan al capital para generar nuevos intereses en los siguientes periodos.
Por supuesto, puede ser el tiempo que se desee, pero comúnmente se manejan:
- Mensualmente.
- Bimestralmente.
- Trimestralmente.
- Semestralmente.
- Anualmente.
Nota: en el ejemplo anterior, era mensualmente.
Frecuencia de capitalización
En pocas palabras, es el número de veces que el interés se capitaliza en un año. Por ejemplo, una tasa que capitaliza mensualmente tiene una frecuencia de capitalización de 12. Esto es debido a que un año tiene 12 meses, entonces su frecuencia de capitalización es de 12.
Ahora bien, si fuese bimestralmente, entonces el periodo de capitalización es bimestral (porque cada dos meses se van a sumar intereses) y la frecuencia de capitalización es de 6. Es 6 debido a que un año tiene 6 bimestres.
¿Cuál sería la frecuencia de capitalización si la tasa capitaliza semestralmente?
¿Por qué es importante que sepas el periodo y la frecuencia de capitalización?
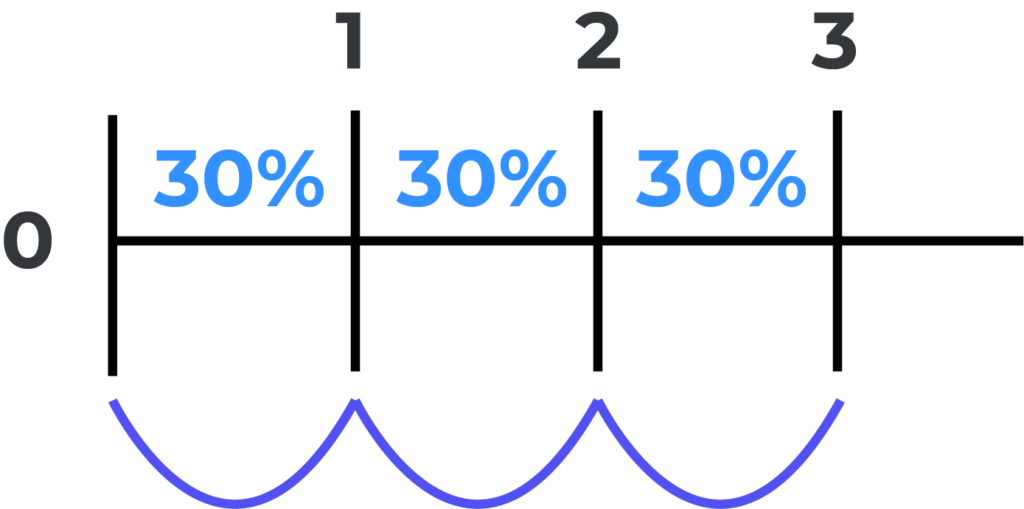
Imagina que le pides prestado dinero a alguien y lo haces a una tasa del 30% mensual. Como ya hemos visto, cada mes se van a generar intereses. Para que veas de una manera más gráfica, voy a ponerte la siguiente imagen.
Como ya hemos visto, cada mes se van a generar intereses. En este caso, la tasa es del 30%, sin embargo, no siempre te van a dar una tasa mensual. Por ejemplo, en lugar de ser mensual, te puedo decir que es una tasa del 30% anual que capitaliza mensualmente.
Tal vez al principio parece ser que es lo mismo, pero no es así. Lo que nos están dando en el segundo ejemplo es una tasa de todo el año, pero que cada mes capitalizará. Si quisiéramos saber cuánto va a capitalizar cada mes, tendríamos que dividir la tasa entre su «frecuencia de capitalización».
En este caso, queda de la siguiente forma:
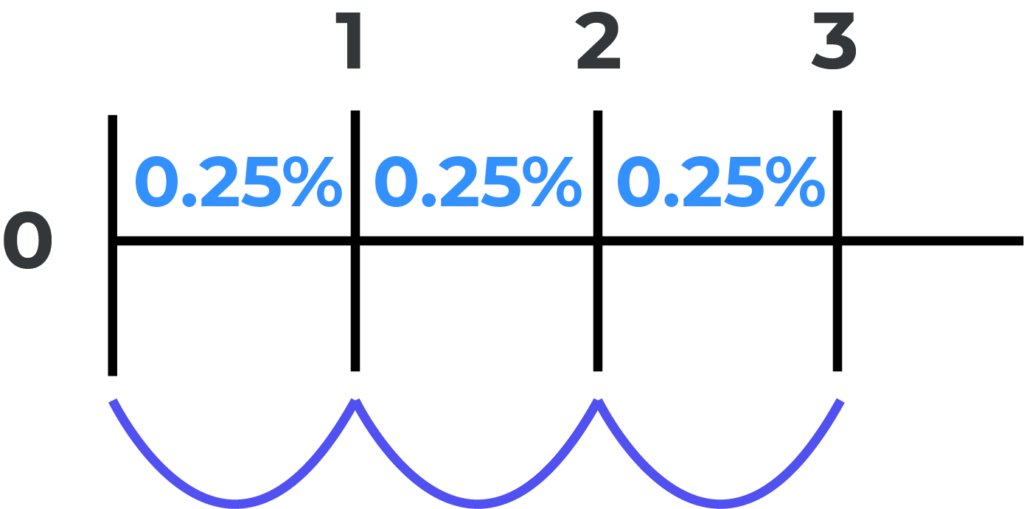
Por lo cual, la respuesta es: 0.0025 o 0.25%. Gráficamente se puede ver de la siguiente forma:
Como puedes ver, no es lo mismo una tasa que capitaliza mensualmente a una tasa anual que capitaliza mensualmente. De hecho, muchas veces puedes salir relativamente engañado si no tomas eso en cuenta.
Nota importante 👈
Las tasas compuestas pueden ser divididas únicamente entre su propia frecuencia de capitalización. Por ejemplo, una tasa que capitaliza semestralmente sólo puede ser dividida entre 2, ya que 2 es su frecuencia de capitalización.
Te recomiendo que repases muy bien los conceptos que he mencionado.
Otro aspecto importante que tienes que tomar en cuenta es que el tiempo y la tasa tienen que estar siempre en la misma nomenclatura. Tal vez no tenga que recordarte esto, debido a que también es una regla de oro en interés simple, pero no está de más recordarlo.
Ecuaciones que se usan en interés compuesto
Sé que con la ecuación de monto ya podrías despejar y obtener lo que necesitas, pero aún así te voy a dejar todos los despejes.
Ecuación para obtener el monto en interés compuesto 👈
Ecuación para obtener el capital en interés compuesto 👈
También se puede ver la ecuación como un cociente, pero depende de la forma en que te acomodes.
Ecuación para obtener la tasa de interés en interés compuesto 👈
Ecuación para obtener el tiempo en interés compuesto 👈
Ejemplo 1 de interés compuesto
Ya tenemos todo lo necesario para poder comenzar a realizar ejercicios de interés compuesto. El primer ejemplo es el siguiente: Se depositan $20,000 en un banco a una tasa de interés del 18% anual capitalizable mensualmente. ¿Cuál será el monto acumulado en tres años?
Procedimiento
Si sustituimos los datos en la ecuación de monto, obtenemos lo siguiente:
Por lo tanto, la respuesta es: $34182.79
Consideraciones
- Cuando obtenemos el monto, lo que estamos haciendo es llevar una cantidad en el tiempo. En el ejemplo, lo que estamos haciendo es llevar los $20,000 pesos a tres años.
- Como es una tasa anual que capitaliza mensualmente, necesitamos encontrar lo que me van a estar dando por mes, por lo cual, se va a dividir la tasa (18%) entre su frecuencia de capitalización (12). Por eso se divide 0.18 entre 12.
- Se pone 36 y no 3 debido a que el tiempo se refiere a las veces que capitaliza mi tasa en el periodo que estoy buscando. Al ser tres años, una tasa mensual capitaliza 36 veces (12 x 3).
Ejemplo 2 de interés compuesto
Se contrató un préstamo bancario por $150,000 pesos. El plazo es de tres años. La tasa de interés es del 20% anual convertible semestralmente ¿Cuál es la cantidad que deberá liquidarse si se decide cancelarlo en forma anticipada a los 15 meses?
Procedimiento
La respuesta es: 190,358.805
Explicación
- La tasa se divide entre 2 debido a que la frecuencia de capitalización es 2 (un año tiene 2 semestres).
- la n es igual a 2.5 debido a que tienes que recordar que n (tiempo) es igual a las veces que la tasa capitaliza en el periodo. Para encontrarlo de manera sencilla, tienes que dividir 15 entre 6. Esto es igual a 2.5.
Consideración
No quiero hacer este artículo más largo y por eso quiero dividirlo en 2 partes. En la siguiente parte voy a continuar con los ejemplos, pero ejemplos en donde se va a tomar en cuenta lo siguiente:
- Inom (tasa nominal).
- ief (tasa efectiva).
- ieq (tasa equivalente).
Si quieres continuar aprendiendo sobre interés compuesto, entonces puedes pulsar el siguiente enlace: tasa nominal, efectiva y equivalente
¡Aprender sobre tasas!
¡Leer más!