Por lo cual, en este artículo vas a aprender lo necesario para que puedas empezar a resolver problemas con interés simple y después vas a poder subir de nivel y comenzarás con interés compuesto y anualidades.
¡Pronto te convertirás en un maestro de las matemáticas financieras!
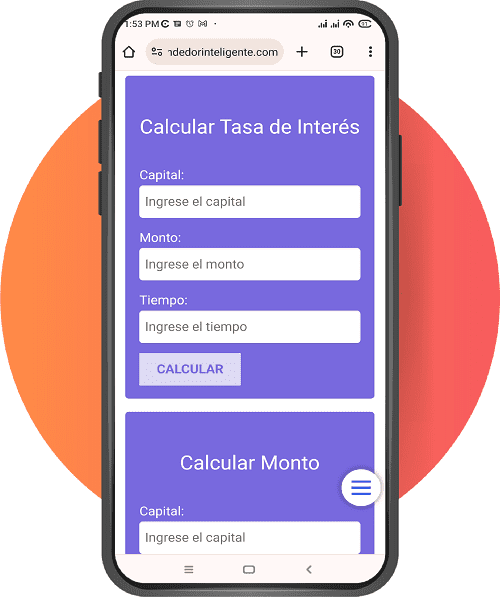
A continuación, te voy a dejar el link de un artículo en el cual vas a poder tener una calculadora de interés simple que te ayudará a calcular el monto, el capital, la tasa de interés o el tiempo de manera sencilla:
¿Qué es el valor del dinero en el tiempo?
Antes de entrar en el tema del interés simple, debemos entender un concepto fundamental: el valor del dinero en el tiempo. Este concepto se basa en que el dinero va cambiando su valor con el paso del tiempo, lo que nos lleva a entender que lo que puedes comprar hoy con una cantidad de dinero no es lo mismo que podías comprar en el pasado o que podrás comprar en el futuro.
Para que quede más claro, te pondré un ejemplo.
Supongamos que hace 15 años disponías de 100,000 pesos y querías comprar un automóvil nuevo. Con esa cantidad, podías adquirir un vehículo nuevo. Sin embargo, en la actualidad, con esos mismos 100,000 dólares, solo podrías comprar un automóvil usado de menor calidad y con más años de antigüedad.
Ahora, proyectemos esta situación hacia el futuro. Dentro de 20 años, si aún dispones de los mismos 100,000 pesos, es probable que ya no puedas adquirir un automóvil en absoluto, ya que el aumento de los precios de los vehículos y la inflación habrán reducido significativamente el poder adquisitivo de tu dinero.
Con esto nos damos cuenta de que el valor del dinero va cambiando a lo largo del tiempo, perdiendo poder adquisitivo, es decir, la capacidad que tiene el dinero para comprar bienes y servicios. Y aquí es donde entra uno de los principios de las finanzas que es lograr que el dinero no pierda su valor, y ¿cómo lo hace? Invirtiendo el dinero para que lo que puedas comprar hoy con una cantidad de dinero sea lo mismo que puedas comprar en unos años.
Cuando el dinero no se invierte y va perdiendo su valor en el tiempo se le llama pérdida de valor adquisitivo. Para poder invertir nuestro dinero de la mejor manera es que vamos a necesitar aprender diferentes conceptos como lo es el interés simple o el interés compuesto.
¿Qué es el interés?
Podemos decir que el interés es el dinero que se paga o se recibe por el uso del dinero ajeno. Es decir, cuando le prestas dinero a alguien o cuando te prestan dinero a ti, hay un costo o un beneficio por ese préstamo. Ese costo o beneficio se llama interés.
Por ejemplo, si le prestas $1,000 pesos a tu amiga y le cobras un 10% de interés, significa que tu amiga te tiene que devolver $1,100 pesos al final del plazo. Es decir, tu amiga te paga $100 pesos por el uso de tu dinero. Ese es el interés que tú recibes por prestarle tu dinero.
Pero si tú le pides prestado $1,000 pesos a tu amigo y te cobra un 10% de interés, significa que tú le tienes que devolver $1,100 pesos al final del plazo. Es decir, tú le pagas $100 pesos por el uso de su dinero. Ese es el interés que tú pagas por pedirle prestado su dinero.
Como puedes ver, los intereses pueden ser un costo o un beneficio, dependiendo de si eres el que presta o el que pide prestado.
¿Cuáles son los tipos de interés?
Existen dos tipos de interés: el Interés simple y el interés compuesto. Sin embargo, en este artículo me voy a concentrar únicamente en el interés simple.
Para que puedas aprender sobre el interés compuesto, entonces te voy a dejar el siguiente artículo:
Definición de interés simple según autores
A continuación, te voy a compartir la definición de interés simple según autores. Por supuesto, al final del artículo vas a encontrar la bibliografía por si estás interesado en comprar algún libro de matemáticas financieras.
Definición de interés simple según Héctor Manuel Vidaurri Aguirre
«El interés simple es aquel en el que sólo el capital gana intereses» (2017, p.121).
Vidaurri Aguirre
Definición de interés simple según Hugo M. Zendejas Núñez
En el caso de Zendejas Núñez, la definición que nos otorga es la siguiente:
«El interés simple es el importe que se cobra al final de cada periodo señalado y que es constante, porque la deuda o capital siempre es el mismo» (2001, p.38)
Hugo M. Zendejas Núñez
Definición de interés simple según Alfredo Díaz Mata
La definición de interés simple según Alfredo Díaz Mata es la siguiente:
«Se denomina interés simple a aquel que se paga o se cobra exclusivamente sobre el importe del capital inicial prestado, esto es, el interés ganado no se acumula al capital y, por tanto, el interés que se paga o se cobra permanece constante en todos los periodos que dura la operación al ser calculado exclusivamente sobre el valor del capital inicial» (2020, p.36)
Alfredo Díaz Mata
Definición según Armando Mora Zambrano
«Cuando un capital genera intereses por un determinado tiempo, el interés producido que se reconoce se denomina interés simple» (2016, p.32)
Armando Mora Zambrano
Definición de interés simple según según Alberto Álvarez Arango
«Se dice que una operación financiera se maneja bajo el concepto de interés simple cuando los intereses liquidados no se suman periódicamente al capital; es decir, los intereses no devengan interés» (2013, p.6)
Alberto Álvarez Arango
¿Cómo funciona el interés simple?
Como podemos observar con las definiciones que los diferentes autores nos han proporcionado, el funcionamiento del interés simple es bastante directo y sencillo. Se calcula aplicando una tasa de interés fija sobre un capital inicial durante un período de tiempo específico.
El interés generado en cada período es constante y se calcula simplemente multiplicando el capital inicial por la tasa de interés y por el número de períodos. No hay reinversión de intereses ni acumulación sobre el capital original.
En resumen, el interés simple es una forma lineal de generar ganancias sobre un capital inicial sin que estas ganancias se sumen al capital para generar más intereses en el futuro.
Conceptos básicos de interés simple
A continuación te voy a poner una tabla con los conceptos básicos de interés simple, los cuales son necesarios para que seas capaz de resolver los diferentes problemas a los que te puedas enfrentar.
| Interés: | El interés es una cantidad adicional de dinero que se paga o se gana cuando se toma prestado o se invierte una cierta cantidad de dinero. Es como un «precio» por usar el dinero de alguien más o por permitir que alguien más use tu dinero. El interés se simboliza mediante la letra I o i. |
| Capital: | Cantidad de dinero tomada en préstamo o invertida. Se puede decir que es el valor del dinero en el presente o punto inicial. Se le suele llamar capital, principal, valor actual o valor presente. El capital es el valor del dinero en el momento inicial de la operación financiera. Se simboliza mediante la letra P o C. |
| Tasa de interés: | La tasa de interés es un porcentaje que se aplica a una cantidad de dinero, representando el costo o rendimiento de utilizar o invertir ese dinero durante un período de tiempo determinado. Se simboliza con la letra T o t. |
| Tiempo: | El tiempo es el número de periodos que dura impuesto el capital; es decir, la duración del préstamo o la inversión. El tiempo es el número de unidades de tiempo que transcurren entre la fecha inicial y final de una operación financiera. Se simboliza con la letra n. |
| Monto: | El monto o valor futuro se define como la suma del capital más el interés ganado y se simboliza mediante la letra F o M. El monto es el valor del dinero en el momento final de una operación financiera. |
¿Cuál es la fórmula del interés simple?
La primera fórmula que tienes que tener en cuenta para resolver problemas de interés simple es la siguiente:
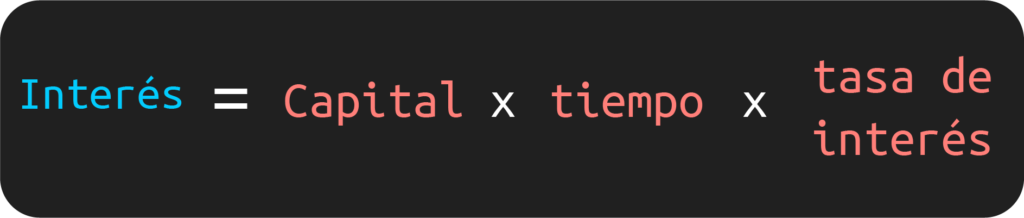
Es decir, la siguiente fórmula.
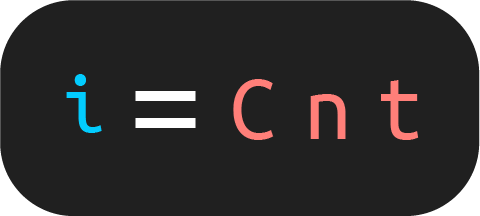
Despejes de la fórmula de interés simple
De la fórmula anterior puedes hacer diferentes despejes para encontrar el capital, el tiempo o la tasa de interés. Los despejes quedan como sigue:
1. ¿Cómo encontrar el capital en interés simple?:
Si lo que quieres calcular es el capital, entonces puedes utilizar la siguiente fórmula:
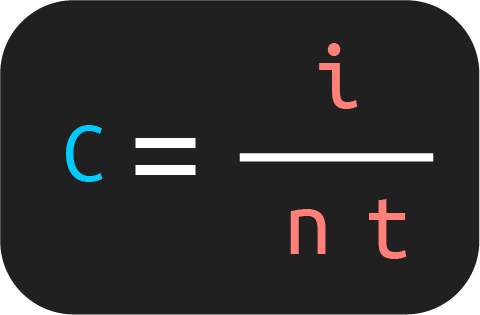
2. ¿Cómo calcular el tiempo en interés simple?
En el caso de que deseas obtener el tiempo, entonces, puedes utilizar el siguiente despeje:
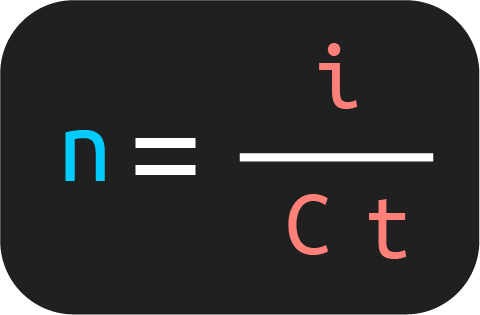
3. Para calcular la tasa de interés
Por último, si lo que quieres es calcular la tasa de interés, entonces, puedes utilizar el siguiente despeje:
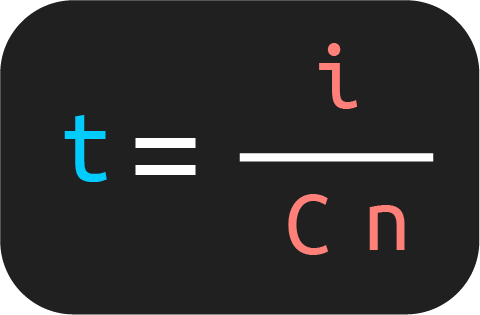
Fórmula para calcular el monto en interés simple
La segunda fórmula que tienes que tener en cuenta en el interés simple es la que involucra al monto. El monto o valor futuro se define como la suma del capital más el interés ganado. Por lo cual, la fórmula queda como sigue:
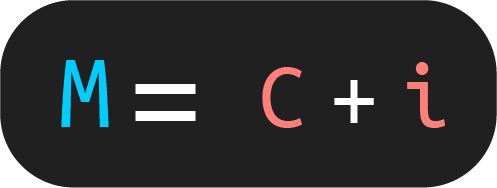
Otra forma en la que podrás encontrar la fórmula del monto es la siguiente:
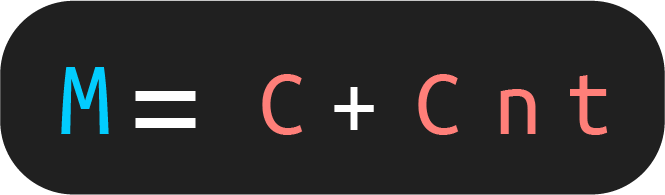
¿Recuerdas cómo se calculan los intereses? Bueno, es multiplicando el capital por el tiempo por la tasa de interés. Justamente eso es lo que pasó en la segunda forma para calcular el monto. Se sustituyó la i (intereses) por su fórmula (Capital x tiempo x tasa de interés).
De tal forma que si no conoces el interés, pero sí conoces el capital, el tiempo y la tasa de interés, entonces podrás calcular el monto.
Por ende, la forma más común en que puedes encontrar la fórmula de monto en interés simple es la que obtienes al factorizar la forma anterior. Al factorizar queda de la siguiente forma:
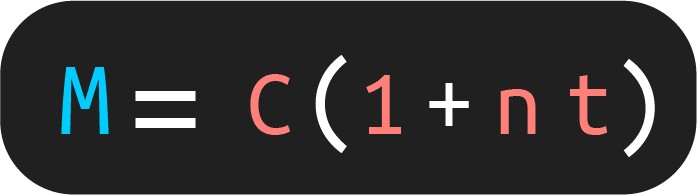
Despejes de la fórmula de monto
Al igual que con la primera fórmula, hay diferentes despejes que te van a ayudar a encontrar lo que necesites:
- Capital.
- Monto.
- Tiempo.
- Tasa de interés.
1. Fórmula para obtener el capital
Si lo que quieres obtener es el capital, entonces, usa el siguiente despeje:
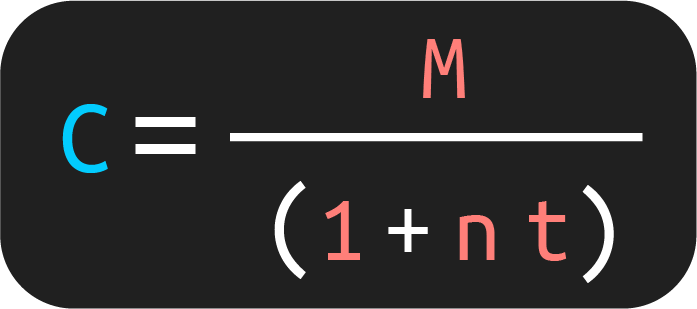
2. Fórmula para obtener el tiempo
Si lo que quieres es obtener el tiempo, entonces, utiliza el siguiente despeje:
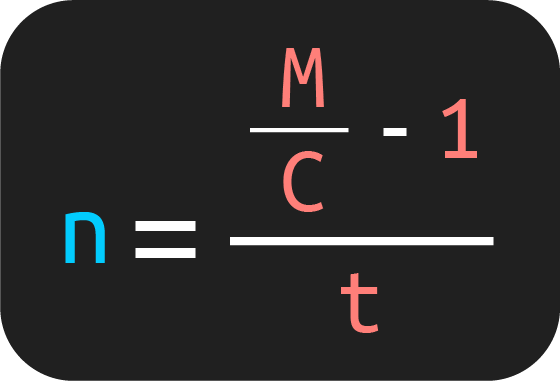
3. Fórmula para obtener la tasa de interés
Por último, si lo que quieres es obtener es la tasa de interés, puedes usar el siguiente despeje:

Con esto ya vas a poder resolver cualquier problema que se te presente de interés simple. Por lo tanto, vamos a pasar a los ejercicios.
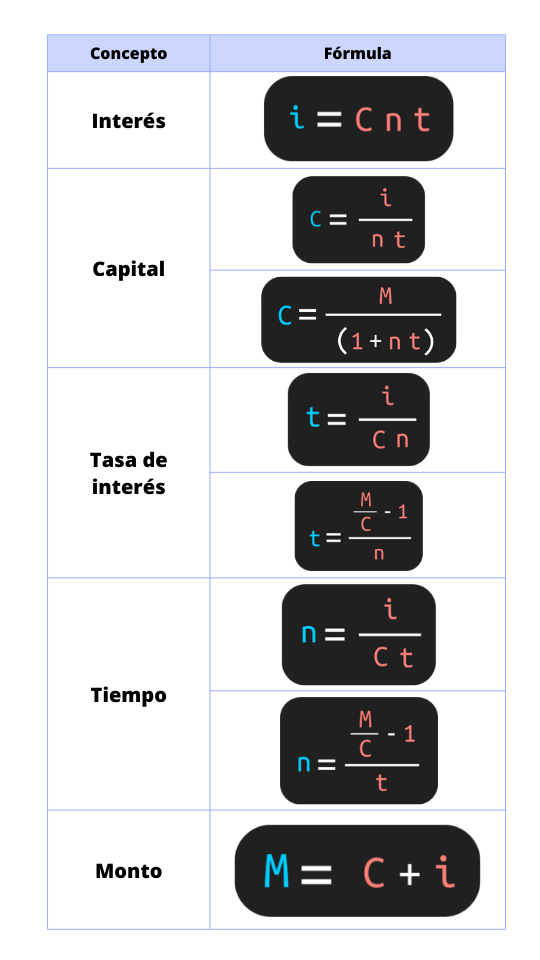
Fórmulas de interés simple
A continuación, te voy a dejar todas las fórmulas de interés simple en una imagen. Puede ser más práctico de esa forma a la hora de resolver los ejercicios.
Si deseas descargar el formulario de interés simple en pdf, puedes pulsar la siguiente imagen:
Regla importante para resolver problemas de interés simple de manera correcta ⛔️
Cuando nos enfrentamos a la resolución de problemas de interés simple, es crucial tener en cuenta dos variables fundamentales: el tiempo y la tasa de interés. Garantizar que ambas estén expresadas en la misma unidad de medida es esencial.
Por ejemplo, si estamos manejando el tiempo en meses, la tasa de interés también debe estar en términos mensuales. Del mismo modo, si estamos trabajando con años, tanto el tiempo como la tasa de interés deben estar en años.
Esto es imprescindible para evitar errores y asegurar que nuestros cálculos sean precisos. En consecuencia, podemos optar por convertir la tasa o el tiempo según sea necesario (según nuestras preferencias) para mantener esta consistencia.
Esta regla básica se resume en la premisa de que la tasa y el tiempo siempre deben estar expresados en la misma unidad de medida. Ten muy en cuenta eso, ya que muchas veces los errores al resolver los problemas tienen que ver con este hecho.
Ejercicios resueltos de interés simple
A continuación voy a poner algunos ejercicios resueltos de interés simple para que puedas practicar un poco.
Ejercicio 1 de interés simple
Si haces una inversión, ¿En cuánto tiempo se va a duplicar tu inversión si se considera una tasa del 50% anual simple?
Para poder resolver el siguiente ejercicio de interés simple, en primer lugar vamos a ver con qué datos contamos.
| Capital: | $100 |
| Monto: | $200 |
| Tasa de interés: | 50% anual simple |
| Tiempo: | ? |
¿De dónde obtuve el capital y el monto? El problema no nos otorga el monto y el capital, pero no importa en este problema. De hecho, puedes escoger las cantidades que tú quieras. Lo único que tienes que respetar es que el monto sea el doble del capital.
Después de todo, te están preguntando sobre el tiempo en que se va a duplicar tu inversión, es decir, ¿En cuánto tiempo el monto será el doble del capital?
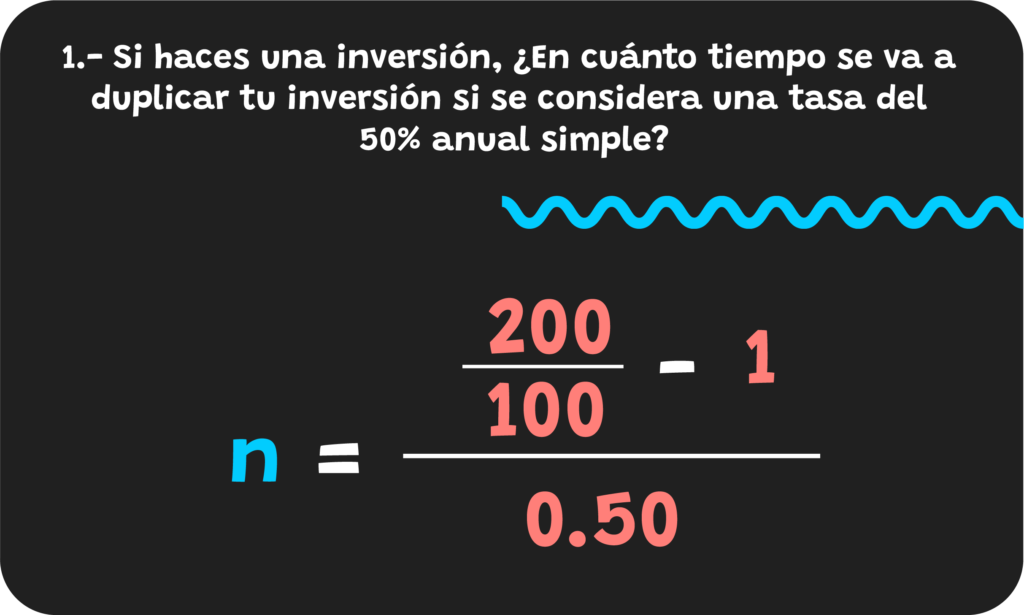
Ahora sólo nos queda sustituir los datos en el despeje de tiempo y vamos a obtener el resultado que buscamos.
Respuesta del ejercicio 1
La respuesta del ejercicio 1 es 2 años. Por lo cual, te tardarías 2 años (24 meses) en duplicar tu inversión.
Ejercicio 2 de interés simple resuelto
¿Cuánto tiempo te tardarías en obtener $10,000 si depositas hoy $2,000 en un fondo que paga 5% de interés simple mensual?
¿Cuáles son los datos que nos otorga el problema?
| Capital: | $2,000 |
| Monto: | $10,000 |
| Tasa de interés: | 5% mensual simple |
| Tiempo: | ? |
Para resolver el ejercicio se tiene que utilizar la misma fórmula que en el ejercicio anterior.
Respuesta del ejercicio 2

Por lo tanto, tardarías 80 meses en obtener los 10,000 pesos. Por cierto, el resultado está en meses porque la tasa de interés es mensual. Podrías obtener el resultado en años, semestres, bimestres o lo que se quiera si se modifica la tasa de interés.
Por ejemplo, si quisiera el tiempo en años, lo que se puede hacer es multiplicar la tasa de interés por 12 (cantidad de meses que tiene un año). De tal forma que tendría que multiplicar 5% por 12 y el resultado es 60%.
Por lo cual, en lugar de poner la tasa de interés como 0.05, ahora se tiene que utilizar 0.6
De tal forma que el resultado en años es 6.67. También puedes usar una regla de tres para convertir los 80 meses en años y vas a obtener el mismo resultado.
Ejercicio 3 de interés simple resuelto
Alejandra compra un teléfono que cuesta $20,000 pesos. Si Alejandra da un pago inicial de $5,000 pesos y acuerda pagar otros $18,000 pesos 12 meses después. ¿Cuál fue la tasa de interés simple que acordó?
Para resolver el problema contamos con los siguientes datos:
| Capital (C): | $15,000 |
| Monto (M): | $18,000 |
| Tiempo (n): | 12 meses |
| Tasa de interés (t): | ? |
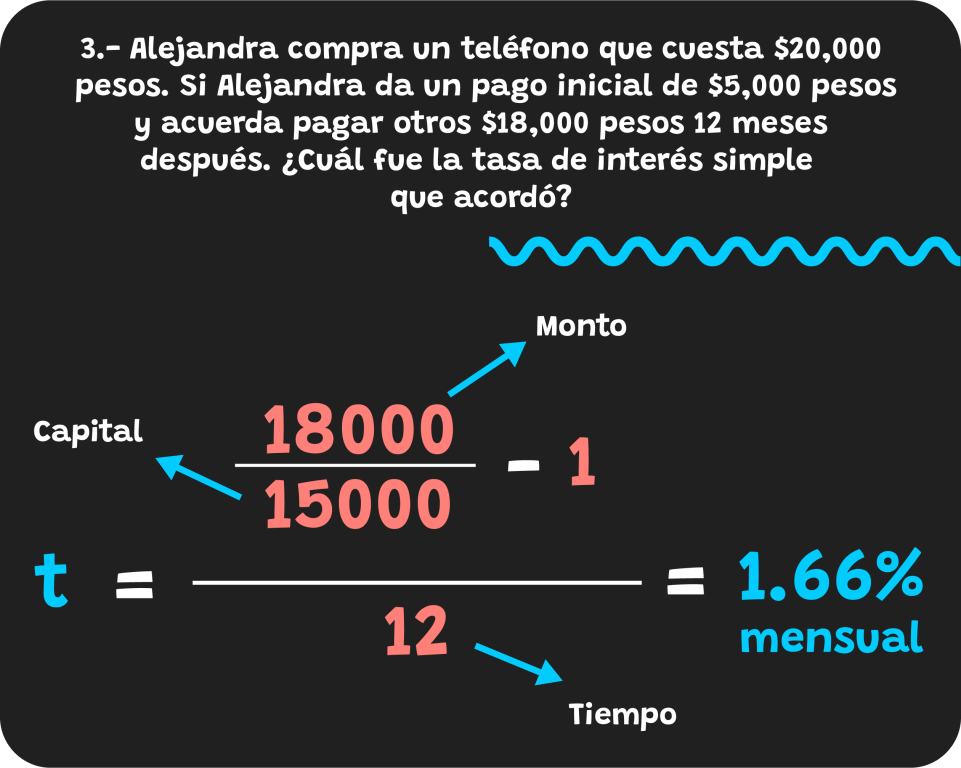
Por lo cual, para resolver el problema se va a utilizar el despeje de tasa de interés.
Respuesta del ejercicio 3
Por lo tanto, la tasa de interés simple es de 1.66% mensual. Al igual que en el ejemplo anterior, gracias a que el tiempo está en meses, entonces, la tasa de interés resultante es mensual.
Ejercicio 4 de interés simple resuelto
Alejandra obtiene un préstamo de $100,000 pesos y tiene que pagarlo 18 meses después. Alejandra acepta un interés simple mensual del 5%. ¿Cuánto deberá de pagar de intereses cada mes?
Son datos con los que contamos para resolver el cuarto ejercicio son los siguientes:
| Capital (C): | $100,000 |
| Tiempo (n): | 18 meses |
| Tasa de interés (t): | 5% mensual |
| Intereses (I): | ? |
Te recomiendo que, antes de que veas la respuesta del ejercicio, intentes resolverlo.
Respuesta del ejercicio 4
Posiblemente te preguntes: ¿No eran 18 meses? Recuerda que el ejercicio está pidiendo el interés mensual. Por lo cual, no es necesario usar la fórmula de monto (aunque también podríamos hacerlo y restarle el capital al resultado).
Ejercicio 5 de interés simple
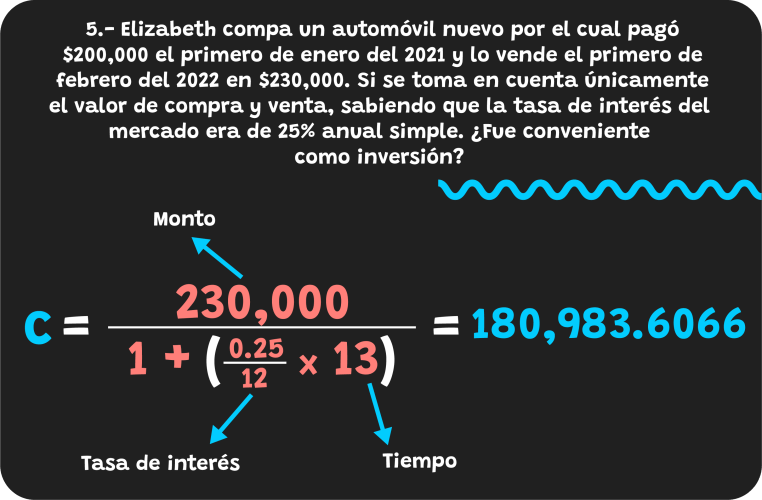
Si Elizabeth compra un automóvil nuevo por el cual pagó $200,000 el primero de enero del 2021 y lo vende el primero de febrero del 2022 en $230,000. Si se toma en cuenta únicamente el valor de compra y venta, sabiendo que la tasa de interés del mercado era de 25% anual simple. ¿Fue conveniente como inversión?
Los datos con los que contamos son los siguientes:
| Monto (M): | $230,000 |
| Capital (C): | $200,000 |
| Tiempo (n): | 13 meses |
Respuesta del ejercicio 5
Para saber si algo fue mejor o peor que otra cosa, lo que tenemos que hacer es una comparación. Si no se hace una comparación con otra cosa, entonces, no podemos decir si fue bueno, malo, mejor o peor.
En este problema nos otorgan una tasa de interés (25% anual simple) para que hagamos la comparación. Por lo cual, podemos utilizar la fórmula de tasa de interés con los datos que nos dan y ver qué tasa de interés es más atractiva.
Aunque, no es la única forma de obtener la respuesta. Para que veas que no es la única forma de resolver este problema, lo voy a resolver de dos formas.
Una primera forma de saber si fue una buena o mala inversión consiste en traer al presente (capital) los 230,000 pesos que le pagan. Por supuesto, utilizando la tasa de interés del mercado (25%). De tal forma que como resultado obtenemos que con 180,983.6066 pesos, hubiésemos obtenido los mismos 230,000 pesos.
Por lo tanto, no fue conveniente la transacción.
Nota: la tasa de interés se divide entre 12 porque quiero obtener mi tasa en meses, ya que el tiempo está en meses. Recuerda que el tiempo y la tasa de interés siempre tiene que estar en la misma nomenclatura.
Ahora lo voy a resolver mediante la tasa de interés.
Como el tiempo está en meses, la tasa de interés resultante es mensual. Por lo tanto, sólo queda multiplicar la tasa por 12 y nos sale que la tasa simple anual es de: 13.8461%
Como puedes ver, la tasa de interés es más baja y por ende, no fue conveniente la inversión.
Nota: el resultado sale 0.01153846154, pero al multiplicarlo por 100 (para obtener el porcentaje) sale 1.153846154% mensual. Ahora bien, para obtener la anual, sólo tienes que multiplicar el resultado por 12.
Ejercicio 6 de interés simple
Marcela va a recibir en 12 meses la cantidad de $50,000 pesos. ¿Cuál es la cantidad que tiene que invertir hoy para obtener dicha cantidad, teniendo en cuenta que la tasa de interés contemplada es del 15% anual simple?
Los datos con los que contamos son los siguientes:
| Monto (M): | $50,000 |
| Tasa de interés (t): | 15% anual simple |
| Tiempo (n): | 12 meses |
| Capital (C): | ? |
Respuesta del ejercicio 6
Por lo cual, se tendría que invertir hoy $43478.26087 pesos para obtener $50,000 pesos en 12 meses a una tasa de interés del 15% anual simple.
Ejercicio 7 de interés simple
Pedro deposita $200,000 pesos en un fondo de inversión bursátil, el cual garantiza un rendimiento del 10% mensual. Si Pedro retira su depósito 30 días después, ¿Cuánto dinero va a recibir?
Los datos que se tienen son:
| Capital (C): | $200,000 |
| Tiempo: (n): | 30 días |
| Tasa de interés (t): | 10% mensual |
| Monto (M): | ? |
Respuesta del ejercicio 7
Por lo cual, se van a recibir $220,000 pesos.
Nota: Recuerda que la tasa de interés se divide por 30 porque nos dieron una tasa mensual y el tiempo está en días. Por ende, se divide la tasa entre 30 para obtener la tasa de interés diaria.
Ejercicio 8: Calcular el monto
La señora García tiene una deuda de $8000 que ya incluye intereses y debe pagarla dentro de 6 meses. Si realiza un pago de $4000 dentro de 3 meses, ¿Cuánto deberá pagar al cabo de los 6 meses si se considera una tasa de interés simple del 25% anual?
Los datos que se tienen son:
| Monto (M): | $8000 |
| Tiempo: (n): | 6 meses |
| Tasa de interés (t): | 25% mensual |
Respuesta del ejercicio 8
Este ejercicio tiene un poco de trampa, ya que para obtener el resultado correcto, tenemos que pensar un poco más en el problema.
En primer lugar, tenemos que tomar en cuenta que la señora García dio un pago de 4000 pesos tres meses después de pedir prestado los 8000 pesos. Ahora bien, tenemos que tener siempre presente que el valor del dinero va cambiando a través del tiempo.
Por lo cual, ya que los 8000 pesos se encuentra en el mes 6 y los 4000 pesos se encuentran en el mes 3, entonces lo que tenemos que hacer es llevar los 4000 pesos al mes 6.
Una vez que tengamos los 4000 pesos en el mes 6, lo único que quedaría es hacer una resta para saber cuánto dinero resta para liquidar la deuda.
A continuación, te voy a mostrar el procedimiento para resolver el ejercicio 8 de interés simple.
Por lo cual, la señora García tiene que pagar 3750 pesos.
Ejercicio 9: Calcular el monto
Si depositas 4000 pesos en una cuenta bancaria que te paga el 6% anual de interés simple, ¿Cuánto dinero tendrás al cabo de 5 años?
Los datos que se tienen son:
| Capital (C): | $4000 |
| Tiempo: (n): | 5 años |
| Tasa de interés (t): | 6% anual simple |
Respuesta del ejercicio 9
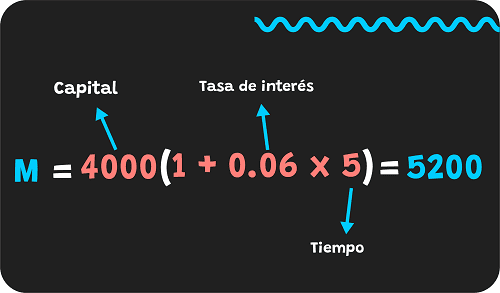
Para resolver este ejercicio, tenemos que usar la fórmula del monto: M=C(1 + tn)
- Sustituimos los valores que tenemos en la ecuación:
M=4000(1+0.06×5)
- Simplificamos y obtenemos:
M=5200
- Por lo tanto, el dinero que tendrás será de 5200 pesos.
Ejercicio 10: Calcular la tasa de interés
Si pides un préstamo de $10,000 pesos a un amigo y le pagas $12,000 pesos al cabo de 8 meses, ¿Qué tasa de interés simple te ha cobrado?
Para poder resolver este problema de interés simple, contamos con los siguientes datos:
| Capital (C): | $10000 |
| Monto (M): | $12000 |
| Tiempo (n): | 8 meses |
Respuesta del ejercicio 10
- Para resolver este ejercicio, tenemos que despejar la tasa de interés de la fórmula del monto y sustituir los datos. Al hacerlo, obtenemos lo siguiente:
- Por lo tanto, la tasa de interés es del 2.5% mensual. Cabe destacar que el resultado que vas a obtener al resolver la ecuación es de 0.025, pero si deseas obtener el resultado en porcentaje, entonces tienes que multiplicarlo por 100. Por eso yo he puesto 2.5%.
Ejercicio 11: Calcular el monto
Si compras una bicicleta de 8000 pesos a crédito y te cobran el 15% semestral de interés simple, ¿Cuál será el monto que tendrás que pagar si liquidas tu deuda en 2 años?
| Capital (C): | $8000 |
| Tasa de interés (t): | 15% semestral |
| Tiempo (n): | 2 años o 4 semestres |
Respuesta del ejercicio 11
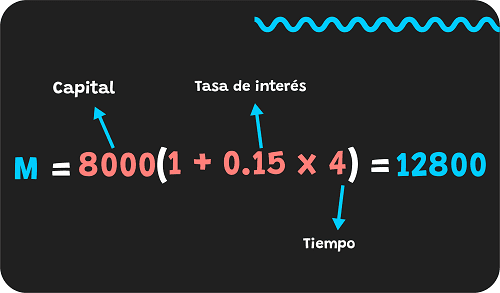
- Para resolver este ejercicio, tenemos que usar la fórmula del monto: M=C(1 + tn)
- Sustituimos los valores que tenemos:
M=8000(1+0.15×4)
- Simplificamos y obtenemos:
M=12800
- Por lo tanto, el monto que tendrás que pagar será de 12800 pesos.
Nota: Para resolver correctamente este ejercicio, tenemos que considerar la regla que nos dice que el tiempo y la tasa de interés tienen que estar expresadas en la misma unidad de medida. Por lo cual, tenemos que convertir el tiempo a semestres o convertir la tasa semestral a una tasa anual. En este caso, yo pase el tiempo a semestres.
Ejercicio 12: Calcular el tiempo
Si inviertes 5000 pesos al 12% trimestral de interés simple, ¿cuánto tiempo tardarás en duplicar tu dinero?
Los datos con los que contamos son los siguientes:
| Capital (C): | $5000 |
| Tasa de interés (t): | 12% trimestral |
| Monto (M): | $10000 |
Respuesta del ejercicio 12
Para poder resolver este ejercicio hay que leer bien el problema, ya que no nos dan de manera directa el monto, el cual vamos a necesitar. Sin embargo, sí nos lo están dando de manera indirecta, ya que nos están pidiendo el tiempo en que tardamos en duplicar los 5000 pesos, es decir que el monto es de 10000.
Teniendo lo anterior en mente, lo único que tenemos que hacer es sustituir los datos en la ecuación y con eso tenemos el resultado.
Como puedes ver, tardarías 8.3333 trimestres en duplicar tu dinero. Son trimestres ya que ocupamos una tasa de interés trimestral. Si lo queremos en meses, tenemos que tardaríamos al rededor de 24.9999 meses.
Ejercicio 13: Calcular el interés
Si recibes 6000 pesos como regalo y los prestas al 18% anual de interés simple, ¿cuánto interés habrás ganado después de 15 meses?
Los datos con los que contamos son los siguientes:
| Capital (C): | $6000 |
| Tasa de interés (t): | 18% anual |
| Tiempo (n): | 15 meses |
Respuesta del ejercicio 13
- Para resolver este ejercicio, tenemos que usar la siguiente fórmula: I=M−C
- Pero antes, tenemos que calcular el monto con la otra fórmula:
M=C(1+in)
- Sustituimos los valores que tenemos:
M=6000(1+0.015×15)
Cabe destacar que no me he equivocado al poner 0.015, ya que lo que hice fue dividir la tasa de interés anual (0.18) entre 12 meses para obtener una tasa mensual.
- Ahora vamos a simplificar y obtenemos:
M=7350
- Ahora, sustituimos el monto en la fórmula del interés simple:
I=7350−6000
- Simplificamos y obtenemos:
I=1350
- Por lo tanto, el interés que habrás ganado será de 1350 pesos.
Ejercicio 14: Calcular el monto
Si te prestan 2000 pesos al 12% mensual de interés simple, ¿cuánto tendrás que pagar si devuelves el dinero en 4 meses?
Los datos con los que contamos son los siguientes:
| Capital (C): | $2000 |
| Tasa de interés (t): | 12% mensual |
| Tiempo (n): | 4 meses |
Respuesta del ejercicio 14
- Para resolver este problema, tenemos que usar la fórmula del monto:
M=C + I
- Pero antes, tenemos que calcular el interés simple con la otra fórmula:
I=C×t×n
- Sustituimos los valores que tenemos:
I=2000×0.12×4
- Simplificamos y obtenemos:
I=960
- Ahora, sustituimos el interés simple en la fórmula del monto:
M=2000+960
- Simplificamos y obtenemos:
M=2960
- Por lo tanto, tendrás que pagar 2960 pesos.
¿Quieres más ejercicios de interés simple resueltos?
A continuación, te voy a proporcionar otros problemas de interés simple que te ayudarán a practicar. Para resolver los siguientes ejercicios, te recomiendo que tengas en cuenta la siguiente fórmula. Claro que voy a poner ejercicios variados.

Dicha fórmula te ayudará a resolver todos los ejercicios que siguen, pero tienes que hacer los despejes que sean necesarios para encontrar lo que te piden en el problema.
Ejemplo 1 de interés simple
Determinar cuánto debe pagarse de interés por un préstamo de $78,000 al 36% anual durante tres años en interés simple.
Los datos que tenemos son:
| Capital (C): | $78,000 |
| Tasa de interés (t): | 36% anual |
| Tiempo (n): | 3 años |
| Intereses (i): | ? |
Ocupando la fórmula tenemos lo siguiente:

Por lo tanto, el interés que deberá de pagarse es de $84,240 pesos.
Cabe aclarar que no debes de utilizar la tasa de interés en %, sino que tienes que dividir el porcentaje por 100 y esa es la cifra que vas a utilizar. De hecho, en algunos libros se utiliza la T como la tasa de interés en porcentaje y la t como tasa de interés después de dividirla entre 100.
Ejemplo 2 de interés simple
Al comprar un automóvil se pactó pagarlo en 2 años a una tasa de 36% anual y se pagaron $7,800 por intereses. ¿Cuánto costó el automóvil?
Los datos que tenemos son:
| Tiempo (n): | 2 años |
| Tasa de interés (t): | 36% anual |
| Intereses (i): | $7800 |
| Capital (C): | ? |
Como puedes ver, tenemos que usar el despeje del capital para poder resolver el problema y queda de la siguiente forma:

Por lo tanto, el automóvil costó $10,833.33
Ejemplo 3 de interés simple
En un préstamo por $300,000 se pagaron en 4 años de plazo $128, 000 de intereses. ¿Cuál fue la tasa de interés pactada?
Los datos que tenemos son:
| Capital (C): | $300,000 |
| Tiempo (n): | 4 años |
| Intereses (i): | $128,000 |
| Tasa de interés: | ? |
Si usamos el despeje para obtener la tasa de interés obtenemos:

Para obtener en porcentaje la tasa de interés, únicamente tenemos que multiplicar el resultado por 100. Por lo tanto, la tasa de interés que se pactó fue del 10.66%
Ejemplo 4 de interés simple
¿Cuál fue el tiempo que estuvo impuesto un capital de $250,000, a una tasa de 18.50% anual y que generó intereses por $175,000?
Los datos que tenemos son:
| Capital (C): | $250,000 |
| Tasa de interés (t): | 18.5% anual |
| Intereses (i): | $175,000 |
| Tiempo (n): | ? |
Por lo tanto, para resolverlo vamos a usar el despeje para obtener el tiempo y obtenemos:

Este ejercicio tiene algo interesante y es el hecho de que 3.7838 años es la respuesta correcta, pero… ¿3.78 años? Probablemente quieres algo más concreto, es decir, años, meses y días.
Por lo tanto, partes de que ya tienes 3 años y quieres saber cuánto es 0.7838 en meses. Así pues, lo único que tienes que hacer es multiplicar 0.7838 por 12 (cantidad de meses) y el resultado es 9.4056. Así pues, son 9.4056 meses.
Ahora bien, si quieres continuar y obtener los días, lo único que tienes que hacer es multiplicar 0.4056 por 30 (días en un mes). El resultado es 12.168.
Por lo tanto, la respuesta completa es 3 años, 9 meses y 12 días
Ejemplo 5 de interés simple
Bueno, realmente todos los ejercicios han estado muy sencillos… ¿verdad? Bueno, pondré un ejercicio simple, pero con una pequeña trampa en la que podemos llegar a caer si nos distraemos un poco.
¿Cuál es el interés que produce un capital de $150,000, al 38% anual en 6 meses?
Los datos que tenemos son:
| Capital (C): | $150,000 |
| Tasa de interés (t): | 38% anual |
| Tiempo (n): | 6 meses |
| Interés (i): | ? |
Como puedes ver, la tasa de interés es anual y el tiempo está en meses. Por lo cual, para obtener la respuesta correcta tenemos que convertir la tasa de interés o el tiempo de tal forma que ambas queden en años, meses o días. Es decir, deben de tener la misma medida de tiempo.
En este caso, yo voy a convertir la tasa de interés anual a una tasa de interés mensual y nos da:
- T = 3.166% mensual
- t = 0.03166
Una vez hecho eso, ya podemos utilizar la fórmula y obtenemos lo siguiente:

Bueno, tengo que aclarar una cosa muy importante, al dividir 38 / 12 (para obtener la tasa mensual), el valor real es de 19/6, lo que es igual a 3.166666667 y tendríamos que dividir 19/6 entre 100 para poder utilizar esa tasa en la fórmula. Por lo tanto, la tasa que tendríamos que utilizar es: 19/600 (0.03166666667).
Digo esto debido a que al no ocupar el valor real, el resultado puede variar. Tanto es así que utilizando 19/600 en la fórmula, el resultado correcto es el de $28,500. Por 6 pesos no te puede cuadrar algo. Por lo tanto, procura utilizar fracciones.
Bueno, por ahora son todos los problemas sobre interés simple que he preparado. Espero que te hayan sido de utilidad. Por cierto, si tienes algún ejercicio que quieras que agreguemos al artículo, no dudes en dejarlo en los comentarios.
Ejemplo 6
Juan invierte $10,000 en un certificado de depósito a una tasa de interés simple del 3.5% anual. Si decide retirar el dinero después de 2 años, ¿cuánto recibirá en total?
Solución
En este caso, utilizamos la fórmula del monto de interés simple para poder resolver el problema.
M = C (1 + t * n)
Donde:
- M = Monto (el total a recibir)
- C = Capital (cantidad inicial invertida)
- t = Tasa de interés anual
- n = Tiempo.
Sustituyendo los valores, tenemos los siguiente:
- M = 10000 * (1 + 0.035 * 2)
- M = 10000 * (1 + 0.07)
- M = 10000 * 1.07
- M = 10700
Por lo cual, se va a recibir un total de 10,700 pesos en dos años.
Ejemplo 7
María presta $5,000 a su amigo Pedro a una tasa de interés simple del 2% mensual. Pedro devuelve el dinero después de 6 meses. ¿Cuánto tiene que pagarle a María?
Solución:
Utilizando la fórmula del interés simple:
M = C (1 + t * n)
Sustituyendo los valores, tenemos:
- M = 5000 * (1 + 0.02 * 6)
- M = 5000 * (1 + 0.12)
- M = 5000 * 1.12
- M = 5600
Pedro tiene que pagarle a María un total de $5,600 después de 6 meses.
Ejemplo 8
Pedro quiere ahorrar $10,000 para comprar un automóvil dentro de 1 año. Si coloca su dinero en un depósito de renta fija que rinde un interés simple mensual del 1.5%, ¿cuánto debe invertir inicialmente?
Solución del ejercicio 8 de interés simple
Para resolver el ejercicio 8, vamos a tener que utilizar la fórmula para encontrar el capital en interés simple. Te recuerdo que la ecuación del capital es la siguiente:
C = M / (1 + t * n)
Donde:
- M = Monto deseado ($10,000 en este caso)
- C = Capital (cantidad a invertir)
- t = Tasa de interés mensual (0.015 en forma decimal)
- n = Tiempo (en este caso, 1 año o 12 meses)
Sustituyendo los valores en la fórmula, tenemos:
- C = M / (1 + t * n)
- C = 10000 / (1 + 0.015 * 12)
- C = 10000 / (1 + 0.18)
- C = 10000 / 1.18
- C = 8474.576271
Por lo tanto, Pedro debe invertir aproximadamente $8,474.58 inicialmente en su depósito de renta fija para tener $10,000 después de 1 año.
Ejemplo 9
Luis necesita tener $50,000 ahorrados en 3 años para un viaje. Si desea colocar su dinero en un depósito de renta fija que rinde un interés simple anual del 4.2%, ¿cuánto debe invertir inicialmente?
Solución del ejercicio 9 de interés simple
Al igual que en el caso anterior, nos están pidiendo en el ejercicio que encontremos el capital. Por lo cual, vamos a necesitar la fórmula para encontrar el capital en interés simple. Recuerda que la ecuación es la siguiente:
C = M / (1 + t * n)
Sustituyendo los valores en la fórmula, tenemos:
- C = M / (1 + t * n)
- C = 50000 / (1 + 0.042 * 3)
- C = 50000 / (1 + 0.126)
- C = 50000 / 1.126
- C = 44404.97336
Por lo tanto, Luis debe invertir aproximadamente $44,404.98 inicialmente en su depósito de renta fija para tener $50,000 después de 3 años.
Ejemplo 10
En qué tiempo una inversión de $5000 se convierte en $6000 al 10% de interés simple anual.
Solución del ejercicio 10 de interés simple
Como puedes ver, nos están pidiendo encontrar el tiempo. Por lo tanto, para resolver el ejercicio 10 de interés simple, vamos a utilizar la fórmula para encontrar el tiempo. Te recuerdo que la ecuación es la siguiente:
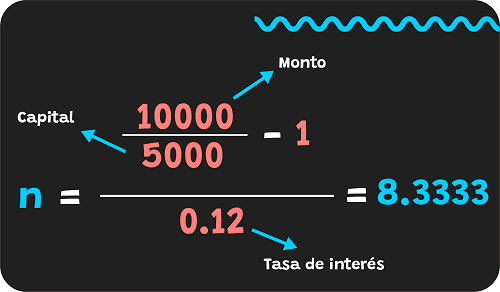
n = (M/C) – 1 / t
Sustituyendo los valores conocidos, tenemos:
- n = (6000/5000) – 1 / 0.10
- n = (1.2) – 1 / 0.10
- n = 0.2 / 0.10
- n = 2
Por lo tanto, una inversión de $5000 se convierte en $6000 en 2 años a una tasa de interés simple anual del 10%.
NOTA: Mi resultado fue anual porque la tasa de interés que nos dieron fue anual. Por lo cual, el resultado que nos va a dar es anual. Si fuese una tasa mensual, entonces el resultado que obtendríamos sería un tiempo en meses.
Ejemplo 11
Una inversión inicial de $5000 se duplica en 3 años. ¿Cuál es la tasa de interés simple anual?
Solución del ejercicio 11 de interés simple
En este caso, nos están pidiendo que encontremos la tasa de interés anual. Por lo cual, basta con sustituir los datos en la ecuación de tasa de interés. Sin embargo, ¿Nos falta algo? No tenemos un monto y lo necesitamos para utilizar la fórmula. ¿Qué hacemos?
Realmente sí nos están dando el monto, aunque no de manera directa. Recuerda que nos están diciendo que el capital se duplica en 3 años. Por lo cual, el monto tiene que ser el doble que el capital. Así pues, si nuestro capital es de 5000 pesos, entonces el monto tiene que ser de 10000 pesos.
Ahora sí podemos comenzar a resolver el ejercicio 11. Te recuerdo que la ecuación para encontrar la tasa de interés en interés simple es la siguiente:
t = (M/C) – 1 / n
Sustituyendo los datos, obtenemos lo siguiente:
- t = (M/C) – 1 / n
- t = (10000/5000) – 1 / 3
- t = (2) – 1 / 3
- t = 1 / 3
- t = 0.333333 o 33.3333%
Por lo tanto, la tasa de interés compuesto simple anual necesaria para duplicar una inversión en 3 años es aproximadamente del 33.3333%.

Calculadora de interés simple
Si lo deseas, a continuación te voy a dejar el enlace a un artículo en donde podrás encontrar una calculadora que te permitirá resolver diferentes problemas de interés simple.
Interés compuesto
Si quieres seguir aprendiendo sobre matemáticas financieras, entonces tienes que seguir con el interés compuesto. A continuación te voy a dejar el enlace del artículo.
Ejercicios resueltos de interés compuesto
Si ya conoces sobre interés simple, ahora es tiempo de que aprendas lo que es el interés compuesto. Si estás buscando algunos ejercicios resueltos, entra al artículo.
Problemas resueltos de interés simple en video
Tengo que decir que no son de mi propiedad los videos que voy a poner de YouTube, sino que pienso que es posible que quieras ver otros ejercicios de interés simple, pero en video. En este caso, voy a utilizar algunos videos pertenecientes al canal de YouTube llamado: «Matemáticas profe Alex»
Si quieres ver más ejercicios, puedes entrar a su canal de YouTube.
¿Cómo calcular interés simple en Excel?
Realmente es muy simple resolver los ejercicios de interés simple, pero si lo deseas, es posible hacer uso de Excel para poder calcular el interés simple de manera automática.
De tal forma que sólo tendrías que sustituir los datos que deseas y obtendrías el valor que te haga falta. A continuación te voy a compartir un video que he encontrado, en el cual te explican de manera sencilla a crear tu plantilla de interés simple.
El video es el siguiente:
Nota: Lo único que le falta que le agreguen es el cálculo de los intereses, pero lo puedes agregar tú mismo. Lo único que tienes que recordar es que los intereses son iguales al monto menos el capital.