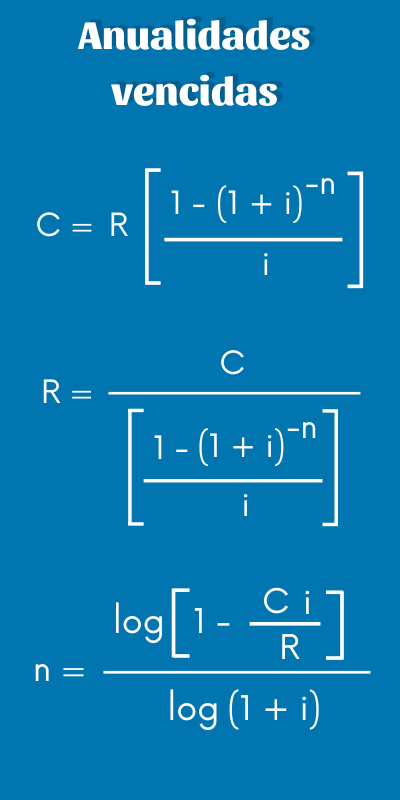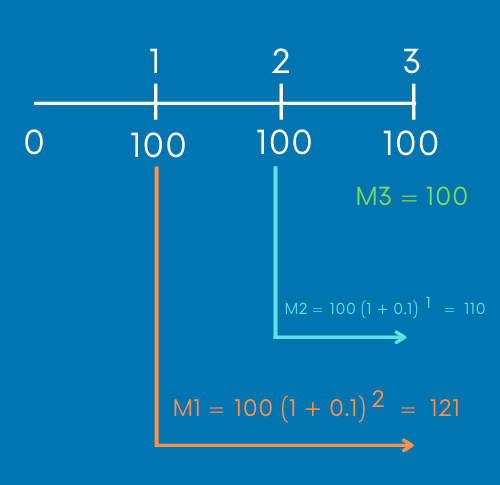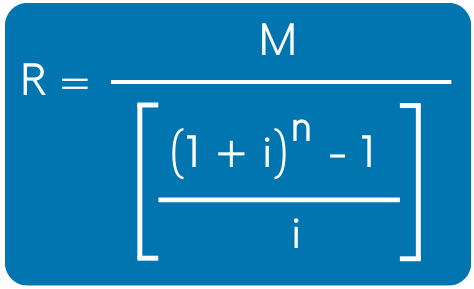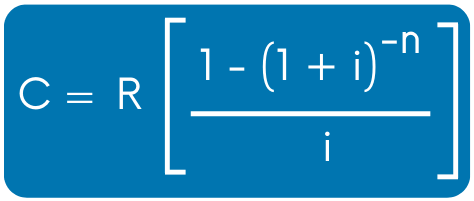Las anualidades pueden clasificarse en diferentes tipos, pero en el artículo de hoy voy a enfocarme en las anualidades vencidas, también llamadas anualidades ordinarias.
De tal forma que al finalizar el artículo sabrás qué es una anualidad vencida y cómo vas a ser capaz de resolver diferentes problemas. Por supuesto, tendrás diferentes ejercicios que te ayudarán a entender el tema de mejor manera.
Espero que te sea de utilidad.
¿Qué es una anualidad?
Una anualidad es una operación financiera que puede ser vista como una serie de pagos que tienen que ser liquidados (realizados) en intervalos iguales (los cuales no siempre tienen que ser anuales) en un plazo acordado por el deudor y acreedor.
Cabe destacar que las cantidades que tienen que ser saldadas no tienen que ser siempre pagos, sino que también pueden ser inversiones que se hacen.
Ahora bien, la definición anterior de anualidad la voy a separar en tres partes (3 conceptos) para que sea más entendible.
¿Cuál es el objetivo de las anualidades?
El objetivo principal de las anualidades es proporcionar una fuente estable y predecible de ingresos a lo largo del tiempo.
Las anualidades pueden ser utilizadas para varios propósitos, tales como planear para la jubilación, financiar la educación, pagar una hipoteca o cualquier otra deuda a largo plazo, o incluso para financiar un negocio.
3 conceptos necesarios para entender el concepto de anualidad
Como dije antes, la definición la voy a separar en tres conceptos que te serán clave para poder entender el funcionamiento de una anualidad y te servirán para resolver problemas.
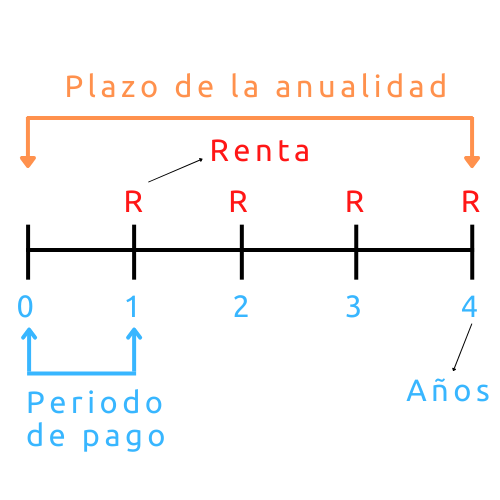
- Renta: es el nombre que se le otorga al pago, depósito o retiro periódico que se hace.
- Intervalo o periodo de pago: es el tiempo que pasa entre un pago y otro.
- Plazo de una anualidad: es el tiempo que transcurre desde la fecha inicial (primer pago), hasta la fecha del último pago.
De tal forma que la anualidad puede ser vista como una serie de rentas que son efectuadas en un mismo intervalo y que son pactadas a un determinado plazo.
Como puedes ver, esos conceptos están en la definición.
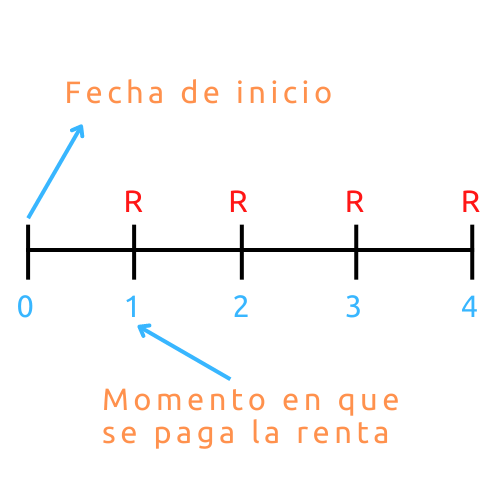
A continuación, te voy a dejar una imagen que te servirá para entender el concepto de anualidad, en donde podrás ver los conceptos que te he dado de manera gráfica.
¿Cómo se clasifican las anualidades?
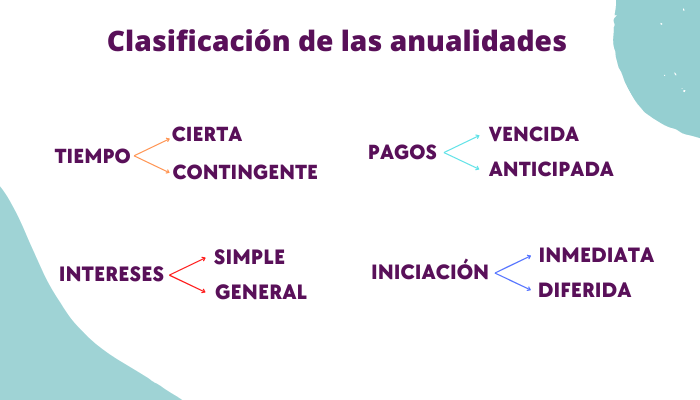
Una anualidad, con base en los elementos que intervienen en ellas se clasifican de la siguiente forma:
Algo importante a resaltar es el hecho de que las categorías no son excluyentes, es decir, una anualidad puede y es una combinación de las cuatro categorías. Por ejemplo, una anualidad puede ser:
- Simple.
- Cierta.
- Vencida.
- Inmediata.
Por lo cual, considero que debo de hablarte de cada categoría, antes de hablar sólo de las anualidades vencidas. Después de todo, la anualidad tendrá que ser una combinación de cada una de las categorías.
De hecho, podríamos hacer un árbol de decisiones para ver todas las posibles combinaciones que se pueden formar.
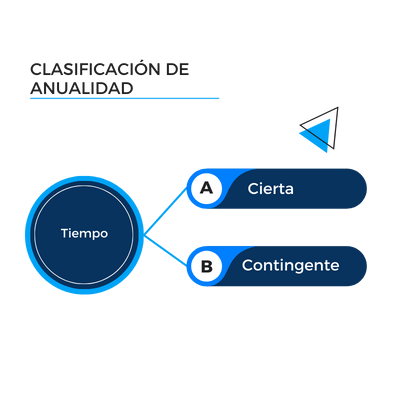
1. Con respecto al tiempo
Con respecto al tiempo, una anualidad se puede clasificar de la siguiente forma:
| Tipo | Concepto |
|---|---|
| Cierta: | Una anualidad es cierta si sus fechas son fijas y si se estipulan con anticipación. Por lo cual, sabemos cuándo inicia y cuándo termina. Por ejemplo, si sacamos el crédito de una casa, sabemos cuándo comenzamos pagar y cuándo vamos a terminar de pagar. |
| Contingente: | En una anualidad contingente no sabemos (no se establece desde el inicio) cuándo será la fecha del primer pago, del último pago o de ambos pagos. Un ejemplo de esto es un seguro de vida, ya que no se sabe cuando será el último pago. |
De tal forma que aquí estamos hablando sobre la iniciación y terminación.
2. Con respecto a los pagos
Con respecto a los pagos, una anualidad puede ser:
| Tipo | Concepto |
|---|---|
| Vencida: | Los pagos tienen que ser realizados al vencimiento del periodo de pago. Se puede decir que yo uso y luego pago. Por ejemplo, si yo saco un producto a crédito y se paga cada mes, entonces no voy a pagar de inmediato, sino que empiezo a pagar un mes después. |
| Anticipada: | Los pagos tienen que ser realizados al principio de cada periodo de pago. En este caso yo pago y luego uso. Si vas a rentar una casa, lo más probable es que tengas que pagar la mensualidad para poder comenzar a utilizar la propiedad. |
3. Con respecto a los intereses
Con respecto a los intereses, una anualidad puede clasificarse en:
| Tipo | Concepto |
|---|---|
| Simple: | El periodo de pago coincide con el periodo de capitalización de los intereses. Por ejemplo, si la tasa de interés es mensual y el periodo de pago es mensual. |
| General: | El periodo de pago no coincide con el periodo de capitalización de los intereses. Por ejemplo, la tasa de interés es semestral y el periodo de pago es mensual. |
4. Con respecto a la iniciación
| Tipo | Concepto |
|---|---|
| Inmediata: | Los pagos o cobros se tienen que hacer en el periodo inmediato a la realización del contrato o trato. |
| Diferida: | Se pospone por un tiempo la realización de los cobros o pagos. Muchas veces se le conoce como periodo de gracia. |
Te voy a poner un ejemplo para que puedas entender mejor. Piensa en que vas a una tienda para comprar los regalos de navidad de tu familia. Ahora bien, no cuentas con el dinero suficiente y vas a sacar los productos a crédito.
Hasta aquí todo normal, ¿cierto? Bueno, ahora voy a ponerte dos situaciones que ejemplifican a una anualidad inmediata y a una simple.
1. Ya sacaste el producto a crédito y te van a cobrar $1000 pesos cada mes por un año. Cabe destacar que vas a comenzar a pagar el siguiente mes. En este caso estamos hablando de una anualidad inmediata porque vas a comenzar a pagar en el periodo inmediato a la realización del préstamo.
2. Tenemos la misma situación que en el caso anterior, pero te dicen que vas a empezar a pagar $1000 pesos cada mes por un año, pero comienzas a pagar hasta enero del 2023 (3 meses después). Por lo cual, te están dando un periodo de gracia, ya que no vas a comenzar a pagar en el periodo inmediato a la realización del trato.
Como puedes ver, ambos casos se pueden dar de manera habitual.

Ejercicios resueltos de anualidades diferidas
En este artículo, te voy a proporcionar diferentes ejercicios resueltos para que aprendas sobre qué son y cómo funcionan las anualidades diferidas.
¿Qué es una anualidad vencida?
Como dije antes, una anualidad puede pertenecer a diferentes categorías, sin embargo, una anualidad es vencida cuando el pago se tiene que realizar al finalizar el periodo, es decir se hace al vencimiento.
Puedes pensar que en las anualidades vencidas se usa y luego se paga. De hecho, cuando compras a crédito haces eso mismo, ya que no pagas de inmediato, sino que empiezas a pagar hasta que finaliza el periodo de pago.
A continuación, te voy a poner una imagen para que te quede más claro:
Diferencia entre una anualidad vencida y una anticipada
Siguiendo con la imagen anterior, si fuese una anualidad anticipada, se tendría que pagar la anualidad desde el inicio, es decir desde el 0 (fecha inicial). Así de simple. ya que en una anualidad anticipada los pagos se hacen al inicio del periodo y no al finalizar.

Ejercicios resueltos de anualidades anticipadas
En este artículo, te voy a proporcionar diferentes problemas resueltos para que aprendas sobre las anualidades anticipadas y cómo funcionan.
¿Qué elementos necesitas para resolver problemas con este tipo de anualidades?
Lo que necesitas conocer es lo siguiente:
- Renta: R
- Capital: C
- Monto: M
Si estás viendo anualidades, entonces considero que ya conoces sobre interés simple y compuesto. Ahí se habla sobre capital, monto, tasa de interés, etc.
Por lo cual, para no hacer más largo el artículo, no voy a explicarlo. Sin embargo, te voy a dejar dos artículos en los cuales lo explico y muestro ejercicios.
Fórmulas de anualidades vencidas
¿Cómo se calcula la anualidad vencida? Las ecuaciones que vas a necesitar para que puedas resolver problemas de anualidades vencidas u ordinarias son las siguientes:
Nota: Los problemas de anualidades pueden ser resueltos simplemente con interés compuesto, pero las ecuaciones antes mencionadas nos permiten hacer las cosas de manera más rápida. Sin embargo, tienes que saber que los problemas con anualidades consideran las sumas de interés compuesto.
1. Fórmulas de anualidades vencidas con el monto
Si deseas obtener el monto, el tiempo o la renta en anualidades vencidas, entonces puedes usar las siguientes ecuaciones:
2. Ecuaciones de anualidades vencidas con el capital
Ahora, a continuación te voy a compartir las fórmulas relativas al capital.
Ejercicios resueltos de anualidades vencidas
A continuación, te voy a proporcionar algunos ejercicios para que aprendas a resolver problemas de anualidades vencidas u ordinarias.
1. ¿Cuál es el monto de $100 mensuales depositados al final de cada mes, durante tres meses en una cuenta bancaria que rinde 10% mensual?
Antes de resolver el problema quiero destacar que he puesto un ejercicio de anualidades vencidas muy sencillo porque voy a resolverlo con interés compuesto y con las fórmulas que te he dado sobre anualidades.
Ahora bien, este problema de anualidad pertenece a las siguientes categorías:
- Cierta: Es una anualidad cierta porque sabemos la fecha final y la de inicio (Son tres meses).
- Simple: Es una anualidad simple porque el periodo de pago coincide con el periodo de capitalización de los intereses. En este caso en ambos es mensual.
- Inmediata: Se trata de una anualidad inmediata porque no mencionan que exista algún periodo de gracia. Por lo cual, se empieza a pagar en el periodo inmediato.
- Vencida: Es una anualidad vencida porque el pago se hace al final de cada mes (final del periodo).
Por lo cual, se trata de una anualidad simple, cierta, inmediata y vencida. Bueno, ahora vamos a resolver el problema.
Datos de ejercicio
Los datos con los que contamos son los siguientes:
| Renta (R): | 100 pesos mensuales |
| Plazo de la anualidad (n): | 3 meses |
| Tasa de interés (i): | 10% mensual |
| Monto (M): | ? |
👉 Resolución del problema con interés compuesto
Si ya aprendiste interés compuesto, entonces sabes que el problema anterior puede ser resuelto con interés compuesto y para hacerlo sólo necesitas usar la fórmula de monto. Sin embargo, ya que se hacen tres pagos, se tienen que tomar por separado y llevar las cantidades a través del tiempo. Por último, sólo se tendría que hacer la suma de las tres cantidades obtenidas.
Claro que tienes que recordar que sólo se tienen que llevar en el tiempo dos cantidades (la renta del primer mes y la renta del segundo mes), ya que la renta del tercer mes se encuentra en la fecha final (hacia donde vamos a llevar las otras dos cantidades).
Para que lo puedas observar mejor, te voy a poner la siguiente imagen:
Ahora, ocupando la ecuación de monto, queda de la siguiente forma:
Como puedes ver, ya tenemos los tres montos. Ahora sólo queda sumar los tres montos y ya tendremos el monto de la anualidad.
Por lo cual la respuesta es: 121 + 110 + 100 = 331
👉 Problema resuelto con las ecuaciones de anualidades vencidas
Ya que estamos buscando el monto, vamos a utilizar la siguiente fórmula:
Es la misma que te compartí más arriba.
Ahora bien, vamos a sustituir los datos:
Como puedes ver, nos sale el mismo resultado, es decir 331. Por lo cual, las ecuaciones de anualidades nos ahorran tiempo, ya que sería tardado resolver problemas con sólo las ecuaciones de interés compuesto.
Asimismo, he resuelto el ejercicio así para que veas cómo se comportan las anualidades.
2. Deseas obtener un capital de $200,000 mediante inversiones semestrales al final de cada semestre, durante 10 años. ¿Cuál es la renta que necesitas depositar si se considera una tasa de interés del 20% semestral?
Vamos a ver con qué datos contamos para poder resolver el ejercicio.
| Monto (M): | 200,000 |
| Plazo de anualidad (n): | 10 años = 20 semestres |
| Tasa de interés (i): | 20% semestral |
| Renta (R): | ? |
vamos a utilizar la ecuación de renta, ya que nos están preguntando sobre la renta que tenemos que dar semestralmente para que en 10 años podamos obtener la cantidad de 200,000 considerando una tasa del 20% semestral.
La ecuación para encontrar la renta de una anualidad vencida es la siguiente:
Si sustituimos los datos queda de la siguiente forma:
Nota: no se ocupa el 10 (años) porque tienes que seguir las reglas que se vieron en interés compuesto. De tal forma que no podemos usar años si la tasa de interés es semestral. Claro que también podemos cambiar la tasa de interés, pero para este ejercicio queda mejor cambiar el plazo a semestres y así obtener la renta semestral.
3. Deseas efectuar una inversión que te permita obtener una renta de $100,000 pesos durante 5 años. Considera una tasa del 40% anual. ¿Cuánto deberás de invertir?
¿Estamos ocupando el monto? No, ya que nos están hablando sobre la inversión, es decir nos están preguntando sobre el capital. De tal forma que contamos con los siguientes datos:
👉 Datos del problema
| Capital (C): | ? |
| Renta (R): | 100,000 anuales |
| Plazo (n): | 5 años |
| Tasa de interés (i): | 40% anual |
👉 Resolución del problema
La fórmula que vamos a utilizar es la siguiente:
Si sustituimos los datos queda de la siguiente forma:
Por lo cual, necesitarías hacer una inversión de 203,516.39 peso para recibir una renta de 100,000 pesos anuales por 5 años.
4. Encuentra el importe pagado (capital) por un aparato electrónico por el cual entregaste un enganche de $1,000. Considera que se hicieron 12 pagos mensuales vencidos por $100. Se considera un interés del 30% anual capitalizable mensualmente.
Los datos con los que contamos son los siguientes:
👉 Datos del problema
| Capital (C): | ? |
| Renta (R): | 100 pesos mensuales |
| Plazo (n): | 12 meses |
| Tasa de interés (i): | 30% anual capitalizable mensualmente |
| Enganche: | 1000 pesos |
👉 Resolución del problema
De momento no hay que hacerle caso al enganche, después de todo, ya se encuentra en el valor actual o presente. Lo que hay que hacer es traer todas los pagos que se hicieron al valor actual o presente (Capital).
Por supuesto, podríamos hacerlo con interés compuesto (fórmula de capital) y traer cada cantidad al presente para luego sumar todas las cantidades. Sin embargo, vamos a utilizar de nuevo la ecuación de capital de anualidades vencidas.
Si sustituimos los datos queda de la siguiente forma:
ahora bien, aún no se termina el problema, ya que no hemos sumado el enganche que se dio. Por lo cual la respuesta es: 1025.77 + 1000 = 2025.77. Ahora sí hemos terminado el problema.
Nota: la tasa de interés se dividió por 12 porque la tasa capitaliza 12 veces en un año, ya que es un año tiene 12 meses. Por lo cual, la tasa de dividió por 12 para encontrar la tasa mensual.
Ejemplos de anualidades vencidas
A continuación, te voy a poner otros ejemplos resueltos de anualidades vencidas para que te quede más claro el tema.
Ejemplo 1 de anualidades vencidas resuelto
1. Una persona desea ahorrar para comprar un automóvil dentro de tres años. Para ello, depositará una cantidad anual de $10,000 en una cuenta que paga una tasa de interés anual del 8%. ¿Cuánto tendrá acumulado al final del tercer año?
Solución únicamente con interés compuesto
Si lo queremos resolver únicamente utilizando interés compuesto, entonces vamos a hacer lo siguiente:
Primero, calculemos el valor futuro de cada uno de los tres depósitos por separado:
- VF1 = 10,000 x (1 + 0.08)^2 = $11,664
- VF2 = 10,000 x (1 + 0.08)^1 = $10,800
- VF3 = 10,000 x (1 + 0.08)^0 = $10,000
Aquí hicimos lo mismo que en el primer ejercicio.
Ahora bien, para obtener el resultado, tenemos que sumar los tres valores futuros que hemos obtenido:
VF Total = VF1 + VF2 + VF3 = $11,664 + $10,800 + $10,000 = $32,464
Por lo tanto, la persona tendrá acumulado $32,464 al final del tercer año.
Solución con las fórmulas de anualidades vencidas
Ahora vamos a resolver el ejemplo con las fórmulas de anualidades vencidas. Ya que en el ejemplo nos están pidiendo calcular el monto, vamos a utilizar la fórmula del monto. Si sustituimos los datos en la fórmula, obtenemos lo siguiente:
Como puedes ver, obtenemos el mismo resultado. De hecho, si no lo obtienes, entonces algo se hizo mal.
Ejemplo 2 de anualidades vencidas
2. Una empresa desea obtener un préstamo de $100,000 y acuerda pagar $20,000 anuales durante cinco años. Si la tasa de interés es del 10%, ¿cuál será el valor presente del préstamo?
Solución del ejemplo con interés compuesto
Primero, calculemos el valor presente de cada uno de los cinco pagos por separado:
- VP1 = 20,000 / (1 + 0.10)^1 = $18,181.81818
- VP2 = 20,000 / (1 + 0.10)^2 = $16,528.92562
- VP3 = 20,000 / (1 + 0.10)^3 = $15,026.29602
- VP4 = 20,000 / (1 + 0.10)^4 = $13660.26911
- VP5 = 20,000 / (1 + 0.10)^5 = $12,418.42646
Luego, sumemos los cinco valores presentes para obtener el valor presente total o el capital:
VP Total = VP1 + VP2 + VP3 + VP4 + VP5 = $75815.73542
Ahora te toca a ti resolver el ejercicio con las ecuaciones de anualidades vencidas que te he proporcionado. He tomado todos los decimales para que el resultado sea idéntico al tuyo.
Ejemplo 3 de anualidades vencidas
3. Una persona desea ahorrar para su jubilación, decide depositar al final de cada año 3,000.00 en una cuenta que le ofrece una tasa de interés anual del 8% capitalizable anualmente. ¿Cuánto tendrá en su cuenta después de 20 años?
Solución del ejemplo con las fórmulas de anualidades vencidas
Para este problemas, voy a resolverlo con las ecuaciones de anualidades vencidas. Para resolverlo, basta con sustituir los datos en la ecuación y obtenemos lo siguiente:
Ejercicio 4 de anualidades vencidas
Un estudiante planea ahorrar para pagar sus estudios universitarios. Realizará depósitos mensuales de $500 al final de cada mes durante 4 años. La cuenta de ahorros ofrece una tasa de interés anual del 4%. ¿Cuánto tendrá acumulado al final de los 4 años?
Solución
Vamos a utilizar la ecuación de monto en anualidades vencidas para encontrar la solución del ejercicio 4. Te recuerdo que la fórmula es la siguiente:
M= R [ ((1+i)^n) −1 / i ]
Si sustituimos los datos en la ecuación, obtenemos lo siguiente:
- M= 500 [ ((1+0.04)^4) −1 / 0.04 ]
- M= 500 [ ((1.04)^4) −1 / 0.04 ]
- M= 500 [ (1.16985856 − 1 / 0.04 ]
- M= 500 [ (0.16985856 / 0.04 ]
- M= 500 [ 4.246464 ]
- M= 2123.232
Por lo tanto, al final de los 4 años, el estudiante tendrá $2123.232 acumulados. Para que puedas practicar y confirmes que el resultado es correcto, te recomiendo que lo resuelvas únicamente con interés compuesto.
Ejercicio 5
Un empresario decide invertir en su negocio y realizará depósitos trimestrales de $2,500 al final de cada trimestre durante 6 años. La tasa de interés anual ofrecida es del 2.5% trimestral. ¿Cuánto tendrá acumulado al final de los 6 años?
Solución
En este caso, también nos están pidiendo que obtengamos el monto. Por lo cual, es lo mismo que en el caso anterior.
Para resolverlo, sólo tenemos que sustituir los datos en la ecuación de monto de anualidades vencidas.
- M= 2500 [ ((1+0.025)^24) −1 / 0.025 ]
- M= 2500 [ ((1.025)^24) −1 / 0.025 ]
- M= 2500 [ (1.80872595 − 1 / 0.025 ]
- M= 2500 [ (0.80872595 / 0.025 ]
- M= 2500 [ 32.349038 ]
- M= 80872.595
Ejercicio 6
Supongamos que deseas ahorrar para comprar un automóvil en 5 años. La meta es ahorrar $50,000 mediante depósitos mensuales al final de cada mes, con una tasa de interés del 2% mensual. ¿Cuál debe ser el monto de cada depósito mensual?
Solución
Como puedes ver, en este ejercicio nos están pidiendo que encontremos la renta, ya que nos están pidiendo el valor que tenemos que ir depositando mensualmente. Por ende, la fórmula que vamos a utilizar es la siguiente:
Por cierto, hay otra ecuación que nos permite encontrar la renta, pero no podemos usar la otra porque en este problema nos están dando el monto (no el capital). Por lo tanto, tenemos que usar la ecuación anterior.
Si sustituimos los datos en la ecuación, obtenemos lo siguiente:
- R= M / [ ((1+i)^n) −1 / i ]
- R= 50000 / [ ((1+0.02)^60) − 1 / 0.02 ]
- R= 50000 / [ ((1.02)^60) − 1 / 0.02 ]
- R= 50000 / [ ((3.281030788) − 1 / 0.02 ]
- R= 50000 / [ 2.281030788 / 0.02 ]
- R= 50000 / 114.0515394
- R = 438.3982
Por lo cual, para poder juntar 50000 pesos en 5 años, se tendrían que aportar 438.3982 pesos mensualmente.
Ejercicio 7
Supongamos que deseas obtener una renta de $50,000 pesos anuales durante 4 años. La tasa de interés anual es del 8%. ¿Cuánto deberás invertir?
Solución
En este caso, nos están pidiendo que encontremos el capital, ya que nos están pidiendo que encontremos la cantidad que necesitamos invertir hoy para poder recibir 50000 pesos anualmente.
Por lo cual, para poder resolver el ejercicio, tenemos que utilizar la ecuación de capital en anualidades vencidas, la cual es la siguiente:
Si sustituimos los datos en la fórmula obtenemos lo siguiente:
- C= R [ (1 – (1+i)^-n) / i ]
- C= 50000 [ (1 – (1+0.08)^-4) / 0.08 ]
- C= 50000 [ (1 – (1.08)^-4) / 0.08 ]
- C= 50000 [ (1 – (0.7350298528) / 0.08 ]
- C= 50000 [ (0.2649701472 / 0.08 ]
- C= 50000 [ 3.31212684 ]
- C= 165606.342
Por lo tanto, se necesitan invertir 165,606.342 pesos para poder recibir anualmente 50000 pesos durante cuatro años. Por supuesto, considerando la tasa de interés del 8% anual.
¿Dónde se aplican las anualidades vencidas?
Las anualidades vencidas las podemos llegar a aplicar en una gran variedad de situaciones financieras, donde se requiere un flujo de efectivo constante y regular a partir de una inversión a largo plazo. Algunos ejemplos de donde se aplican las anualidades vencidas son:
- Planificación de la jubilación: una persona que busca una fuente de ingresos para la jubilación puede optar por invertir en una anualidad vencida. Esto le permitirá recibir pagos regulares al final de cada período, lo que puede ayudar a proporcionar una fuente constante de ingresos en la jubilación.
- Financiamiento de proyectos a largo plazo: las empresas pueden usar anualidades vencidas para financiar proyectos a largo plazo, como la construcción de infraestructura o la adquisición de activos.
- Pago de préstamos: algunas personas pueden optar por invertir en una anualidad vencida como una forma de pagar un préstamo a lo largo del tiempo.
- Planificación de la educación: los padres que desean ahorrar para la educación universitaria de sus hijos pueden optar por invertir en una anualidad vencida. Esto les permitirá recibir pagos regulares al final de cada período que pueden ser utilizados para pagar la educación universitaria de sus hijos.
Espero que este artículo te haya servido para poder aprender lo que son las anualidades vencidas en matemáticas financieras.