Uno de los métodos utilizados para asignar tareas es el método húngaro de asignación. Este enfoque se basa en algoritmos matemáticos que ayudan a determinar la asignación óptima de recursos.
¿Qué es el método húngaro de asignación?
El método de asignación, también conocido como el método húngaro, es una técnica utilizada para resolver problemas de optimización en la distribución de tareas y recursos. Este método se enfoca en encontrar la forma más eficiente de asignar recursos limitados a una serie de tareas, con el objetivo de minimizar el costo o tiempo total requerido para completarlas.

¿Qué es una carga de trabajo?
El término «carga de trabajo» se refiere al proceso de asignación de tareas o procesos a diferentes centros de trabajo o unidades de procesamiento. Este procedimiento tiene como objetivo principal optimizar los recursos disponibles, minimizar los costos operativos y asegurar la ejecución eficiente de las actividades planificadas.
Características del método de asignación
El método de asignación presenta tres características fundamentales que lo distinguen:
1. Unicidad
Cada tarea se asigna a un único recurso, y a su vez, cada recurso se dedica exclusivamente a una tarea. Esta singularidad en las asignaciones asegura la máxima eficiencia y claridad en la ejecución de las actividades.
2. Optimización
El objetivo principal radica en encontrar la asignación que minimice el costo o tiempo total requerido para completar todas las tareas. En este sentido, el método busca la máxima eficiencia en la distribución de los recursos.
Después de todo, no hay que olvidar que los recursos con los que cuenta una empresa son limitados y por ende, se tienen que utilizar de manera inteligente.
3. Tabulación
La representación de los costos o tiempos asociados con las posibles asignaciones se lleva a cabo mediante una matriz. Esto nos ayuda a la visualización y el análisis de las opciones disponibles, permitiendo tomar la mejor decisión.
Por supuesto, más adelante podrás ver cuál es la utilidad de la matriz para poder encontrar la mejor forma de asignar las tareas.
¿Cómo funciona el método húngaro de asignación?
Para que pueda explicarte mejor el funcionamiento del método húngaro de asignación, voy a hacer uso de dos problemas resueltos paso a paso. De tal forma que podrás ver cómo funciona y podrás ver que dependiendo del problema, puedes verte en la necesidad de realizar más pasos en el proceso.
Espero que te sean de utilidad.
Problema resuelto del método húngaro de asignación
A continuación, te voy a proporcionar 2 problemas resueltos del método húngaro de asignación para que puedas entender cómo funciona. Espero que te sean de utilidad.
Problema 1 del método húngaro de asignación
Una empresa tiene tres empleados (A, B, C) que deben ser asignados a tres proyectos (1, 2, 3). Cada empleado tiene un costo diferente para cada proyecto, como se muestra en la tabla a continuación. Encuentra la asignación óptima que minimice el costo total.
Paso 1: Creación del tablero de asignación
Creamos una tabla con los costos de asignación para cada empleado a cada proyecto.
| Proyecto 1 | Proyecto 2 | Proyecto 3 | |
|---|---|---|---|
| Empleado A | 5 | 9 | 7 |
| Empleado B | 8 | 6 | 5 |
| Empleado C | 7 | 4 | 6 |
Paso 2: Reducción de filas
Restamos el menor costo de cada fila a todos los elementos de esa fila.
- De la primer fila, el menor costo es el número 5. Por lo cual, tenemos que restarle 6 a cada elemento de esa fila.
- De la segunda fila, tenemos que el menor costo es el 5. Por lo cual, tenemos que restar 5 a cada elemento de la fila.
- Por último, el menor costo de la tercer fila es 4. Así pues, tenemos que restar 4.
Si hacemos las restas correspondientes, la nueva tabla queda como sigue:
| Proyecto 1 | Proyecto 2 | Proyecto 3 | |
|---|---|---|---|
| Empleado A | 0 | 4 | 2 |
| Empleado B | 3 | 1 | 0 |
| Empleado C | 3 | 0 | 2 |
Paso 3: Reducción de columnas
Ahora, tenemos que restar el menor costo de cada columna a todos los elementos de dicha columna.
- En la columna 1, el cero es el menor costo. Por lo cual, tenemos que restarle 0 a cada elemento de la columna.
- En la columna 2, el 0 también es el menor costo. Por lo cual, tenemos que restarle 0 a cada elemento.
- En la tercer columna, el 0 también es el menor costo. Así que tenemos que hacer lo mismo que en los casos anteriores.
Como en este caso, los menores costos de cada columna son el 0, no tenemos que hacer ninguna resta. Por lo cual, la tabla queda igual que la anterior. Cabe destacar que no siempre pasa así. De hecho este es un problema de asignación muy simple.
| Proyecto 1 | Proyecto 2 | Proyecto 3 | |
|---|---|---|---|
| Empleado A | 0 | 3 | 1 |
| Empleado B | 3 | 1 | 0 |
| Empleado C | 3 | 0 | 2 |
Paso 4: Cubrimiento de ceros con la menor cantidad de líneas posibles
Ahora, tenemos que cubrir todos los ceros con la menor cantidad de líneas posibles. En este caso, necesitamos tres líneas. ¿Por qué tres líneas? Porque tenemos una matriz de 3 x 3. Es decir, tenemos 3 empleados y tenemos 3 proyectos.
¿Qué pasaría si fuese una matriz de 4 x 4? Entonces, necesitamos 4 líneas.
Nota: Las líneas pueden ser verticales u horizontales, pero no pueden ser en diagonal. Asimismo, gracias a que es un ejemplo sencillo, se pudieron poner las tres líneas desde un principio, pero no siempre es el caso. De no ser el caso, se tiene que continuar con otros pasos para completar el algoritmo.
Paso 5: Determinar la asignación
Como dije antes, ya que este ejercicio es muy simple, ya tenemos la solución, sin la necesidad de agregar pasos extra.
Podríamos decir que los ceros nos indican quién debe de realizar qué tarea. En este ejemplo, tenemos lo siguiente:
- Empleado A tiene que realizar el proyecto 1.
- Empleado B tiene que realizar el proyecto 3.
- Empleado C tiene que realizar el proyecto 2.
Ahora, para obtener el costo mínimo total, vamos a necesitar ver la primera tabla que hicimos. Tenemos que si el empleado A realiza el proyecto 1, tenemos un costo de 5. En el caso de que el empleado B realice el proyecto 3, entonces tenemos un costo de 5. Por último, si el empleado realiza el proyecto 2, tenemos un costo de 4.
Por lo tanto, el costo total mínimo es: 5+5+4 = 14.
Problema 2
Vamos a hacer un ejercicio muy similar al anterior, pero vamos a tener otros costos. Una empresa tiene tres empleados (E1, E2, E3) que deben ser asignados a tres proyectos (P1, P2, P3).
Encuentra la asignación óptima que minimice el costo total.
Paso 1: Creación del tablero de asignación
Creamos una tabla con los costos de asignación para cada empleado a cada proyecto.
| Proyecto P1 | Proyecto P2 | Proyecto P3 | |
|---|---|---|---|
| Empleado E1 | 10 | 9 | 5 |
| Empleado E2 | 9 | 8 | 3 |
| Empleado E3 | 6 | 4 | 7 |
Paso 2: Reducción de filas
Restamos el menor costo de cada fila a todos los elementos de esa fila.
| Proyecto P1 | Proyecto P2 | Proyecto P3 | |
|---|---|---|---|
| Empleado E1 | 5 | 4 | 0 |
| Empleado E2 | 6 | 5 | 0 |
| Empleado E3 | 2 | 0 | 3 |
Paso 3: Reducción de columnas
Restamos el menor costo de cada columna a todos los elementos de esa columna.
| Proyecto P1 | Proyecto P2 | Proyecto P3 | |
|---|---|---|---|
| Empleado E1 | 3 | 4 | 0 |
| Empleado E2 | 4 | 5 | 0 |
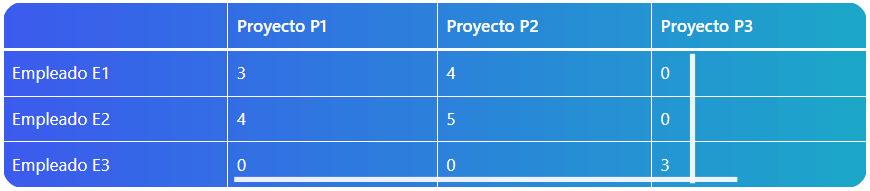
| Empleado E3 | 0 | 0 | 3 |
Paso 4: Cubrimiento de ceros con la menor cantidad de líneas posibles
Ahora, tenemos que cubrir todos los ceros con la menor cantidad de líneas posibles. Si usamos la menor cantidad de líneas posibles para cubrir los ceros, tenemos como resultado que sólo tenemos que utilizar 2 líneas.
Claro que se puede hacer una tercera línea, pero hasta este punto, se tiene que buscar cubrir los ceros con la menor cantidad de líneas posibles. Como se puede ver en la imagen anterior, se pueden cubrir con 2 líneas.
Ahora bien, ya que es una matriz de 3 x 3, necesitamos 3 líneas. Por lo cual, hay que obtener una línea más. ¿Cómo? Vamos a hacer lo siguiente:
Paso 5: Determinar la asignación
Identificamos los valores que no están cubiertos por ninguna línea. En este caso, son el 3, 4, 4 y 5. Ahora bien, una vez que hemos identificado cuáles son los valores que no están tachados por una línea, lo que tenemos que hacer es seleccionar el número que sea menor.
En este caso, el menor número es el número 3.
Ahora bien, una vez hecho lo anterior, tenemos que seguir con el siguiente paso.
Paso 6: Modificación del tablero
Realizamos las operaciones correspondientes según las reglas del Método Húngaro:
- Restamos el menor número no cubierto (el valor que hemos seleccionado en el paso anterior) a los números no tachados. Es decir, tenemos que restarle 3 a todos los valores que no han sido tachados por una línea. De tal forma que tenemos que hacer lo siguiente: 3 – 3; 4 – 3; 4 – 3; y 5 – 3.
- Los números tachados pero no interceptados por líneas permanecen iguales.
- Los números interceptados por líneas se suman. En este problema, el único número que está tachado y que tiene una intercepción es el 3. Correspondiente al empleado E3, Proyecto P3. De hecho, si te das cuenta, pasan dos líneas por ese número. Ahora bien, lo que tenemos que hacer con este valor es sumarle el mismo valor que hemos obtenido en el paso 5, es decir el 3.
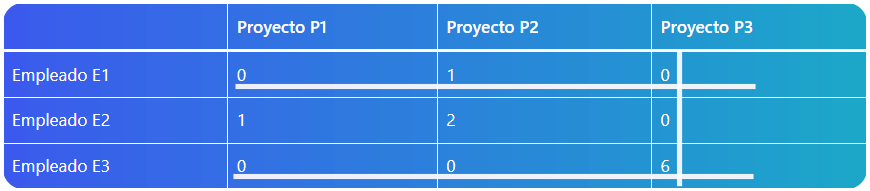
Si hacemos todo lo anterior, obtendremos la siguiente tabla como resultado:
| Proyecto P1 | Proyecto P2 | Proyecto P3 | |
|---|---|---|---|
| Empleado E1 | 0 | 1 | 0 |
| Empleado E2 | 1 | 2 | 0 |
| Empleado E3 | 0 | 0 | 6 |
Paso 7: Colocamos la tercera línea
Necesitamos una línea más para cubrir todos los ceros restantes.
Paso 8: Determinar la asignación final
En pocas palabras, los ceros nos indican qué tareas puede realizar un determinado empleado. En este problema de asignación de tareas, hay dos empleados que pueden realizar dos tareas y un empleado que puede realizar una tarea.
Por lo tanto, vamos a asignarle al empleado que puede hacer una tarea, dicha tarea. De tal forma que el empleado E2 tiene que hacer el proyecto P3.
Ahora bien, nos quedan dos empleados y dos proyectos a asignar. El empleado E1 puede realizar el proyecto P1 y p3, pero ya le asignamos el proyecto P3 al empleado E2. Por lo cual, la única opción disponible es asignar el empleado E1 al proyecto P1.
Siguiendo con esta lógica, tenemos que el empleado E3 puede realizar el proyecto P1 y P2, pero hay que recordar que ya asignamos el proyecto P1 al empleado E1. Por lo cual, el empleado E3 tiene que llevar a acabo el proyecto P2.
Paso 9: Obtener el costo mínimo total.
Determinamos las asignaciones finales y calculamos el costo total mínimo:
- Empleado E1 al Proyecto P1 (costo: 10)
- Empleado E2 al Proyecto P3 (costo: 3)
- Empleado E3 al Proyecto P2 (costo: 4)
El costo total mínimo es: 10+3+4 = 17.
Video explicativo recomendado
La verdad es que hay un video que me ha parecido interesante y corto sobre cómo funciona el método de asignación. El video es el siguiente: