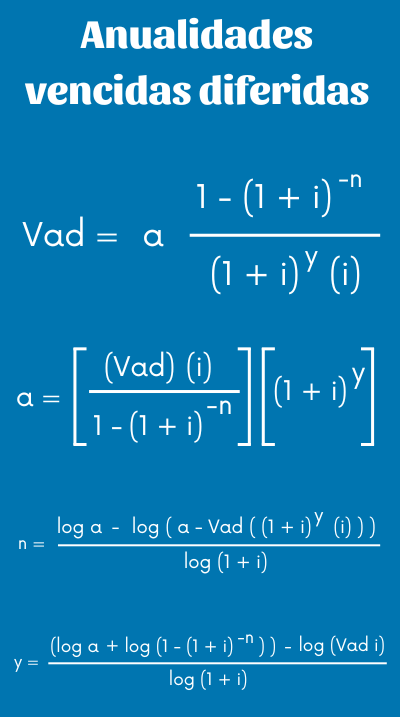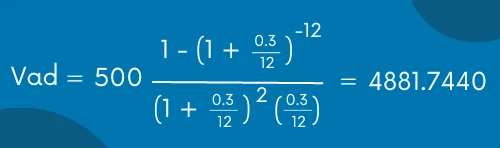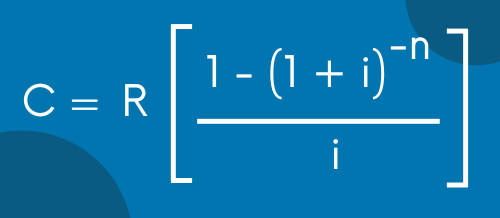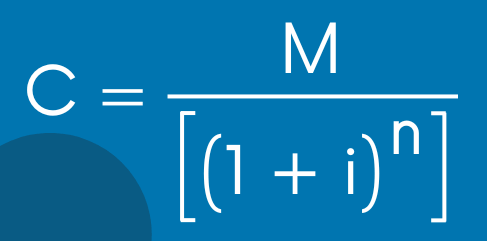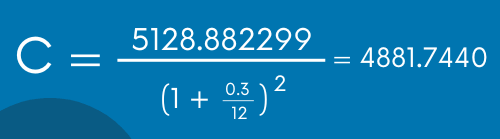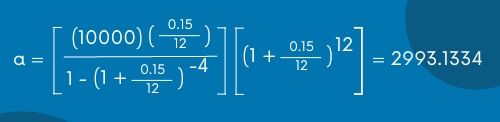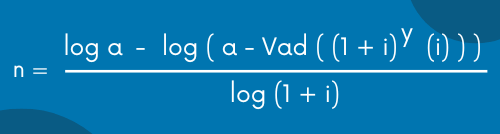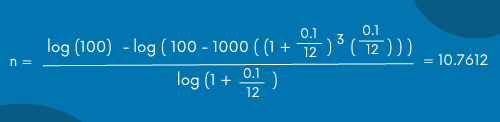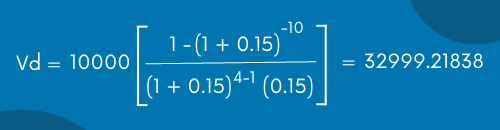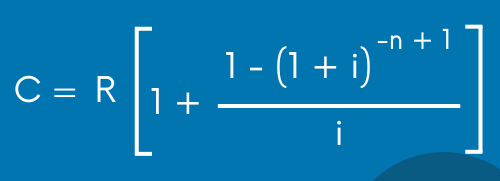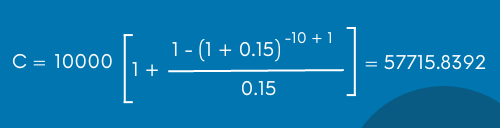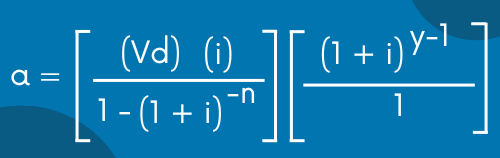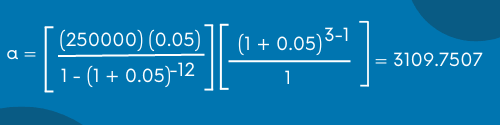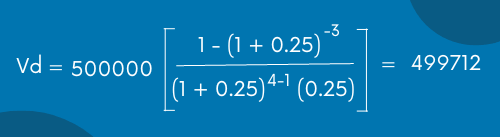En este artículo tengo el objetivo de que aprendas lo que son las anualidades diferidas y pienso que la mejor forma de hacerlo es mediante la resolución de ejercicios. Por lo cual, te voy a compartir un conjunto de ejercicios resueltos que te ayudarán a familiarizarte con el tema.
¿Cómo empezar?
La verdad es que si estás aprendiendo por primera vez lo que es una anualidad, entonces no te recomendaría que siguieras leyendo el artículo. Esto es porque no me voy a detener mucho en explicar los conceptos básicos sobre anualidades o sobre los conceptos básicos sobre interés simple e interés compuesto.
Ahora bien, si ya conoces sobre interés simple y compuesto, entonces yo te recomiendo que empieces a aprender sobre las anualidades anticipadas y sobre las anualidades vencidas. Esto lo digo, ya que es la base para que aprendas a resolver problemas de anualidades diferidas.
A continuación, te voy a dejar dos artículos en los que muestro ejercicios resueltos de anualidades vencidas y anticipadas.
Por cierto, yo te recomiendo que leas los artículos en la siguiente secuencia.
¿Por qué empezar con las anualidades vencidas y anticipadas?
Si ya has leído mi artículo sobre anualidades vencidas, entonces ya sabes que ahí hablo sobre la clasificación de las anualidades y sabrás que una anualidad cae en muchas categorías al mismo tiempo. Por ejemplo, una anualidad puede ser:
- Cierta.
- Simple.
- Anticipada.
- Diferida.
Por lo cual, te vas a encontrar problemas sobre anualidades vencidas diferidas o problemas sobre anualidades anticipadas diferidas. De tal forma que tendrás que conocer su funcionamiento y sus fórmulas para poder resolver los diferentes ejercicios y problemas que se te pongan.
¿Qué son las anualidades diferidas?
Con respecto a la iniciación, una anualidad puede ser inmediata o diferida. Es decir, una anualidad se puede clasificar de la siguiente forma:
- Anualidad inmediata: es inmediata cuando los pagos o cobros se tienen que hacer en el periodo inmediato a la realización del contrato o trato.
- Anualidad diferida: es diferida cuando se pospone por un tiempo la realización de los cobros o pagos. Muchas veces se le conoce como periodo de gracia o periodo de diferimiento.
De tal forma que en las anualidades diferidas el inicio de los cobros (depósitos) o pagos se posponen por uno o más periodos.
¿Te suena complicado? No te preocupes, te lo voy a explicar con algo que seguro te resulta familiar.
Posiblemente hayas visto en alguna tienda alguna promoción como la siguiente: ¡Compre ahora y comience a pagar en tres meses! Bueno, esos tres meses en donde no vamos a pagar nada es a lo que se le suele llamar como periodo de gracia y es la única diferencia que existe entre las anualidades inmediatas (no tienen periodo de gracia) y las anualidades diferidas.
Si aún tienes dudas, no te preocupes, ya que voy a resolver diferentes ejemplos paso a paso de anualidades diferidas (vencidas y anticipadas) para que te quede claro el tema. Por el momento, ten en mente lo del periodo de gracia.
Fórmulas de anualidades diferidas vencidas
Las anualidades diferidas vencidas son aquellas en las que los pagos o cobros se realizan al final de cada periodo, pero se posponen por un tiempo determinado.
Las siguientes fórmulas te van a ayudar a resolver los diferentes problemas de anualidades vencidas diferidas. Las ecuaciones son las siguientes:
- Vad = valor actual
- a = anualidad o renta.
- n = tiempo o número de pagos.
- y = periodo de gracia.
- i = tasa de interés.
Ejercicios resueltos de anualidades diferidas vencidas
Ahora, vamos a utilizar las ecuaciones anteriores para poder resolver algunos problemas sobre las anualidades vencidas diferidas.
Ejercicio 1: ¿Cómo calcular el capital con anualidades diferidas vencidas?
1. Una tienda departamental hace la tan conocida promoción: «Compre ahora y pague después».Tal oferta hace que el 1 de octubre del 2023 hagas la compra de una computadora, por la cual tendrás que pagar 500 pesos mensuales por 12 meses. Considera que tendrás que empezar a pagar a partir del 1 de enero del 2024 y que la tasa de interés es del 30% convertible mensualmente. ¿Cuál es el valor de contado de la computadora?
Los datos con los que contamos para resolver el ejercicio son los siguientes:
| a = | 500 |
| n = | 12 |
| i = | 0.30/12 |
| y = | 2 |
| Vad (valor actual) | ? |
Primera forma para resolver problemas de anualidades vencidas diferidas
Como nos están pidiendo el capital o también llamado valor actual, vamos a ocupar la ecuación del valor actual que te proporcioné anteriormente. Al sustituir los datos en la fórmula obtenemos lo siguiente:
Por lo cual, una forma en la que podrás resolver problemas de anualidades diferidas vencidas es con la ayuda de las ecuaciones que anteriormente te he proporcionado.
Segunda forma para resolver problemas de anualidades diferidas
Los problemas de anualidades diferidas, ya sean vencidas o anticipadas, pueden ser resueltos con las mismas ecuaciones o fórmulas con las que se resuelven los problemas de anualidades vencidas o anticipadas (anualidades inmediatas).
Sin embargo, tenemos que hacer uso también de las ecuaciones de interés compuesto para poder sumar o restar los intereses correspondientes al periodo de gracia. De tal forma que el periodo de gracia es lo único que hace la diferencia entre las anualidades diferidas y las anualidades inmediatas (anualidades anticipadas y vencidas normales).
Para demostrarte lo que acabo de decir, voy a resolver el problema anterior con la fórmula de capital de las anualidades vencidas y con la ecuación de capital de interés compuesto.
¡Vamos a empezar!
Paso 1 para resolver el problema de anualidad diferida vencida de la segunda forma:
Vamos a sustituir los datos con los que contamos en la ecuación de capital perteneciente a las anualidades vencidas (inmediatas). La ecuación es la siguiente:
Si deseas ver todas las fórmulas de anualidades vencidas, entonces pulsa en siguiente botón:
Paso 2
Bueno, ahora vamos a sustituir los datos que tenemos en la ecuación. Al hacerlo obtenemos lo siguiente:
Si fuese un problema de anualidad vencida normal (inmediata), entonces esa sería nuestra respuesta, pero recuerda que en las anualidades diferidas existe un periodo de gracia. En este caso, nos dan un periodo de gracia de 2 meses.
Por lo cual, tenemos que regresar en el tiempo 2 meses la cantidad que obtuvimos. Así pues, lo que vamos a hacer es utilizar la ecuación de capital que viste en interés compuesto y vamos a regresar en el tiempo la cantidad que obtuvimos.
La ecuación para obtener el capital en interés compuesto es la siguiente:
Si sustituimos los datos en la ecuación anterior, obtenemos lo siguiente:
Como puedes ver, el resultado que se obtiene es el mismo, pero en la segunda forma tienes que hacer un paso extra. Por supuesto, la ventaja de la segunda forma es que ya no tienes que memorizar más ecuaciones, ya que son ecuaciones que ya has visto.
Ejercicio 2: Calcular la anualidad en anualidades diferidas vencidas
2. Se depositan $10,000 en un fondo de inversiones con el objeto de retirar 4 mensualidades vencidas a partir del 1 de enero del año 2024. Considera que el periodo de gracia es de 12 meses y que la tasa de interés es del 10% convertible mensualmente, ¿Cuál es el valor de las mensualidades que se podrán retirar?
Los datos con los que contamos son los siguientes:
| C = | 10000 |
| n = | 4 |
| i = | 15% convertible mensualmente |
| y = | 12 |
| a = | ? |
En este caso, ya sólo voy a resolver el problema de la primera forma, pero puedes practicar resolviendo los problemas con las dos formas. Así podrás ver que sale el mismo resultado y podrás seleccionar la opción que te resulte más sencilla.
La ecuación que vamos a utilizar para poder obtener la anualidad o la renta en anualidades diferidas vencidas es la siguiente:
Si sustituimos los datos, obtenemos lo siguiente:
Ejercicio 3
3. Se depositan hoy 1000 en una cuenta de inversiones que paga 10% capitalizable mensualmente, ¿Cuántos retiros mensuales vencidos de 100 se podrán hacer comenzando dentro de 3 meses?
Los datos con los que contamos son los siguientes:
| Vad = | 1000 |
| n = | ? |
| i = | 10% capitalizable mensualmente |
| y = | 3 meses |
| a = | 100 |
La ecuación que vamos a necesitar para resolver este problema es el de el tiempo en anualidades diferidas vencidas. La ecuación es la siguiente:
Ahora sólo queda sustituir los datos en la ecuación y vamos a obtener el resultado.
Fórmulas de anualidades anticipadas diferidas
Ahora te voy a poner las ecuaciones de las anualidades anticipadas diferidas para que puedas resolver los problemas. Las ecuaciones son las siguientes:
En este caso, Vd es igual al valor actual. De ahí en fuera, casi en todas las ecuaciones sólo se le agregó un -1 al periodo de gracia.
Ejercicios resueltos de anualidades diferidas anticipadas
Ahora voy a poner algunos ejercicios resueltos de anualidades diferidas anticipadas.
Ejercicio 1
1. Calcular el valor actual de una renta semestral de $10000 durante 5 años, si el primer pago semestral anticipado se realiza dentro de 2 años. Considera que el interés es del 15% semestral.
Los datos con los que contamos son los siguientes:
| a = | 10000 semestrales |
| n = | 5 años o 10 semestres |
| y = | 2 años o 4 semestres |
| i = | 15% semestral |
| Vd = | ? |
Forma 1 para responder el problema
La primera forma con la que podemos resolver el problema anterior es con la ayuda de las ecuaciones que te proporcioné antes. La ecuación que vamos a utilizar es la del valor actual (Vd).
Por lo cual, si sustituimos los datos obtenemos lo siguiente:
Por lo tanto, el valor actual es igual a 32999.21838
Forma 2 para responder el problema
Como en las anualidades vencidas diferidas, también podemos resolver los problemas usando las fórmulas de las anualidades anticipadas y las ecuaciones de interés compuesto.
A continuación voy a resolver el problema de esa forma.
1. En primer lugar, vamos a utilizar la ecuación para encontrar el capital o valor actual en las anualidades anticipadas (anualidades inmediatas). La ecuación es la siguiente:
Ahora hay que sustituir los datos y obtenemos lo siguiente:
2. Ahora, hay que usar la ecuación de capital que se usa en interés compuesto y obtenemos lo siguiente:
Como puedes observar, obtenemos el mismo resultado que con la forma 1.
Ejercicio 2
2. Deseas adquirir a crédito una nueva computadora para utilizar en tus clases en línea. La computadora tiene un valor de contado de 25000 y si se adquiere a crédito se deberán de dar 12 pagos mensuales anticipados, el primero de los cuales debe de realizarse 3 meses después de la adquisición. Si el interés que se aplica es del 5% mensual, ¿De cuánto serán los pagos que tienes que realizar mensualmente?
Los datos con los que contamos son los siguientes:
| Vd (valor actual) = | 25000 |
| n = | 12 pagos mensuales |
| y = | 3 meses |
| i = | 5% o 0.05 mensual |
| a = | ? |
Para resolver el problema, lo que tenemos que hacer es utilizar la ecuación de anualidad o renta (a) que te proporcioné antes. La ecuación es la siguiente:
Si sustituimos los datos obtenemos lo siguiente:
Ejercicio 3
3. Deseas hacer una inversión que te permita disponer de 500000 al inicio de cada año, durante 3 años, y deseas recibir la primera anualidad a partir del cuarto año de la fecha inicial de la inversión. Considera una tasa de interés del 25% anual. ¿Cuánto tendrás que invertir?
| Vd (valor actual) = | ? |
| n = | 3 años |
| y = | 4 años |
| i = | 25% anual |
| a = | 500000 |
Si sustituimos los datos en la fórmula obtenemos lo siguiente: